主席树(可持久化线段树)
部分可持久化:
可以访问旧版本,但只能修改新版本
完全可持久化:
支持访问,修改旧版本得到答案,修改新版本
汇合可持久化:
在完全可持久化的基础上支持合并
这里的版本一般指一次操作后的状态
而主席树一般支持完全可持久化
【模板】可持久化线段树 1(主席树)
找区间k小值
对于k小值问题,我们很容易想到权值线段树来解决
而对于一个随意的区间要求k小值的话就不太能这么做了
权值线段树:不考虑原序列的顺序,只关心原数的权值
红色字表示该结点维护的权值区间
下方的黑色序列2135167表示原序列
而这棵线段树表示在插入序列所有元素后线段树的节点状态
每个结点上的蓝字表示该结点维护的区间有多少个元素
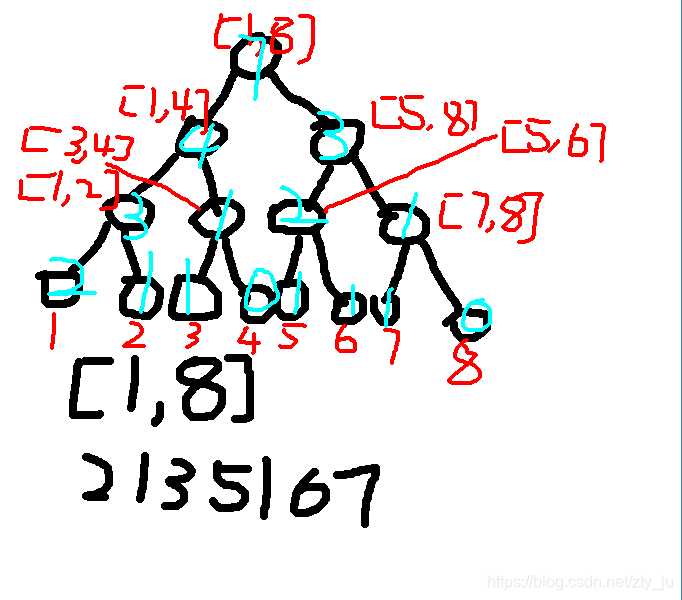
而我们对于单纯的k小值问题,我们的实现代码如下
int query(int k,int rk){
while(1){
int ls=tree[k].ls;
int rs=tree[k].rs;
int mid=l+((r-l)>>1);
if(l==r)
return w[l];
if(tree[ls].sum=rk){
k=ls;
l=l;
r=mid;
continue;
}
rk-=(tree[ls].sum);
k=rs;
l=mid+1;
r=r;
}
}
那么我们能想到用n个前缀的权值线段树像访问前缀和一样去做
也就是我们对于线段树i里面存储了原序列1~i个数的信息
而对于一个区间l~r的信息
我们只需将第r个线段树的所有信息与第l-1个线段树的所有信息相减即能得到
那么问题随即又来了
这里我们需要n^2级别的空间
这肯定是承受不了的
而我们考虑到对于第i棵线段树和第i+1棵线段树
只是加入了a[i+1]这个数
那么应该只改变了logn个节点的信息
而因为主席树需要保证所有线段树信息的完整
所以核心思想就是只加点不改信息
在这个核心思想的指导下
我们对于原来的每一棵完整的线段树
变成加入logn个节点
而其它节点我们就直接让新增的节点指向前一个版本的树节点就好了
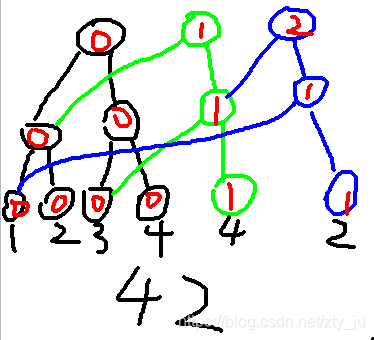
42表示原序列
至此,我们就能愉快的把空间复杂度降至nlogn了
#include <bits/stdc++.h>
using namespace std;
const int maxn=200005;
struct number{
int id,x,rk;
}a[maxn];
struct node{
int ls,rs;
int sum;
}tree[20*maxn];
int n,m,p;
int cnt=0;
int root[maxn];
int w[maxn];
int read(){
int x=0,y=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
return x*y;
}
bool cmp1(number i,number j){
return i.x<j.x;
}
bool cmp2(number i,number j){
return i.id<j.id;
}
void build(int l,int r){
cnt++;
int k=cnt;
if(l==r){
tree[k].ls=tree[k].rs=tree[k].sum=0;
if(l==a[1].rk)tree[k].sum=1;
return ;
}
int mid=l+((r-l)>>1);
int ls,rs;
ls=cnt+1;
build(l,mid);
rs=cnt+1;
build(mid+1,r);
tree[k].ls=ls;
tree[k].rs=rs;
tree[k].sum=tree[ls].sum+tree[rs].sum;
}
void insert(int k2,int l,int r,int val){
cnt++;
int k1=cnt;
if(l==r){
tree[k1].ls=tree[k1].rs=0;
tree[k1].sum=tree[k2].sum+1;//在前一棵树的基础上加一个点
return ;
}
int mid=l+((r-l)>>1);
if(val<=mid){
tree[k1].rs=tree[k2].rs;
tree[k1].ls=cnt+1;
insert(tree[k2].ls,l,mid,val);
}
else{
tree[k1].ls=tree[k2].ls;
tree[k1].rs=cnt+1;
insert(tree[k2].rs,mid+1,r,val);
}
int ls=tree[k1].ls,rs=tree[k1].rs;
tree[k1].sum=tree[ls].sum+tree[rs].sum;
}
int query(int lt,int rt,int rk){
int k1=root[lt-1],k2=root[rt];
int l=1,r=p;
while(1){
int ls1=tree[k1].ls;
int ls2=tree[k2].ls;
int rs1=tree[k1].rs;
int rs2=tree[k2].rs;
int mid=l+((r-l)>>1);
if(l==r)
return w[l];
if(tree[ls2].sum-tree[ls1].sum>=rk){
k1=ls1;
k2=ls2;
l=l;
r=mid;
continue;
}
rk-=(tree[ls2].sum-tree[ls1].sum);
k1=rs1;
k2=rs2;
l=mid+1;
r=r;
}
}
int main()
{
// freopen("testdata.in","r",stdin);
// freopen("ans.out","w",stdout);
n=read();m=read();
for(int i=1;i<=n;i++){
a[i].id=i;
a[i].x=read();
}
sort(a+1,a+n+1,cmp1);
a[0].x=-1e9-1;
for(int i=1;i<=n;i++){
if(a[i].x>a[i-1].x)w[++p]=a[i].x;
a[i].rk=p;
}
sort(a+1,a+n+1,cmp2);
//离散化,将值域降到'n'的级别
build(1,p);
root[1]=1;
//一棵空树
for(int i=2;i<=n;i++){
root[i]=cnt+1;//每棵线段树的根
insert(root[i-1],1,p,a[i].rk);
}
for(int i=1;i<=m;i++){
int l,r,k;
l=read();r=read();k=read();
printf("%d\n",query(l,r,k));
}
return 0;
}
【模板】可持久化数组(可持久化线段树/平衡树)
对于一个数组,我们不知道怎么可持久化
把它升级成更高级的结构——线段树,我们不就会了吗
#include <bits/stdc++.h>
using namespace std;
const int maxn=1000005,maxm=1000005;
struct node{
int ls,rs;
int x;
}tree[20*maxn];
int n,m;
int cnt;
int root[maxm];
int a[maxn];
int read(){
int x=0,y=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
return x*y;
}
void build(int l,int r){
int k=++cnt;
if(l==r){
tree[k].ls=tree[k].rs=0;
tree[k].x=a[l];
return ;
}
int mid=l+((r-l)>>1);
tree[k].ls=cnt+1;
build(l,mid);
tree[k].rs=cnt+1;
build(mid+1,r);
}
void modify(int k2,int pos,int val){
int l=1,r=n;
while(1){
int k1=++cnt;
if(l==r){
tree[k1].ls=tree[k1].rs=0;
tree[k1].x=val;
return ;
}
int mid=l+((r-l)>>1);
if(pos<=mid){
tree[k1].rs=tree[k2].rs;
tree[k1].ls=cnt+1;
k2=tree[k2].ls;
l=l;r=mid;
}
else{
tree[k1].ls=tree[k2].ls;
tree[k1].rs=cnt+1;
k2=tree[k2].rs;
l=mid+1;r=r;
}
}
}
int query(int k,int pos){
int l=1,r=n;
while(1){
int mid=l+((r-l)>>1);
if(l==r)
return tree[k].x;
if(pos<=mid){
k=tree[k].ls;
l=l;r=mid;
}
else{
k=tree[k].rs;
l=mid+1;r=r;
}
}
}
int main()
{
n=read();m=read();
for(int i=1;i<=n;i++)
a[i]=read();
build(1,n);
root[0]=1;
for(int i=1;i<=m;i++){
int v,opt,loc,val;
v=read();opt=read();loc=read();
if(opt==1){
val=read();
root[i]=cnt+1;
modify(root[v],loc,val);
}
else{
root[i]=root[v];
printf("%d\n",query(root[v],loc));
}
}
return 0;
}
递归版本的函数写法
void modify(int x,int y,int l,int r,int p){
if(l>p||r<p)return ;
if(l==r){
tree[x].ls=tree[x].rs=0;
tree[x].sum=tree[y].sum+p;
return ;
}
int mid=l+((r-l)>>1);
tree[x].sum=tree[y].sum+p;
if(p<=mid){
tree[x].ls=++cnt;
tree[x].rs=tree[y].rs;
modify(tree[x].ls,tree[y].ls,l,mid,p);
}
else{
tree[x].rs=++cnt;
tree[x].ls=tree[y].ls;
modify(tree[x].rs,tree[y].rs,mid+1,r,p);
}
return ;
}
int query(int x,int y,int l,int r,int p,int q){
if(l>q||r<p)return 0;
if(l>=p&&r<=q)return tree[y].sum-tree[x].sum;
int mid=l+((r-l)>>1);
int tmp1=query(tree[x].ls,tree[y].ls,l,mid,p,q);
int tmp2=query(tree[x].rs,tree[y].rs,mid+1,r,p,q);
return tmp1+tmp2;
}
[JSOI2018]列队
orz 九条可怜
我们可以证明这样一个小小的结论
我们在[k,k+r-l]这个区间内,一定存在一条分割线
满足该线左边的人就站到该线左边的位置,右边的站在右边的位置
这样一定最优
如果左右两边有两人分别坐标为x,y,x在左,y在右
他们原本的目标位置是u,v,u在左,v在右
现在两人目标位置交换
那么距离和为|x-v|+|y-u|=v-x+y-u
原距离和为|x-u|+|y-v|
若u<=x,v<=y
原式等于x-u+y-v=y-u+x-v<y-u+(-x)+v
若u<=x,v>y
原式等于x-u+v-y=v-u+x-y<v-u-x+y
若u>x,v<=y
原式等于u-x+y-v=y-x+u-v<y-x-u+v
若u>x,v>y
原式等于u-x+v-y=v-x-y+u<v-x+y-u
综上证毕
那么我们直接建个主席树
维护两个信息
坐标和,以及数量
我们二分这个分割线的位置当分割线左边的人正好有从k到分割线这么多个时就找到了
但我被愉快的卡常了
。。。
#pragma GCC diagnostic error "-std=c++14"
#pragma GCC target("avx")
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
#pragma GCC optimize("-falign-labels")
#pragma GCC optimize("-fdevirtualize")
#pragma GCC optimize("-fcaller-saves")
#pragma GCC optimize("-fcrossjumping")
#pragma GCC optimize("-fthread-jumps")
#pragma GCC optimize("-funroll-loops")
#pragma GCC optimize("-fwhole-program")
#pragma GCC optimize("-freorder-blocks")
#pragma GCC optimize("-fschedule-insns")
#pragma GCC optimize("inline-functions")
#pragma GCC optimize("-ftree-tail-merge")
#pragma GCC optimize("-fschedule-insns2")
#pragma GCC optimize("-fstrict-aliasing")
#pragma GCC optimize("-fstrict-overflow")
#pragma GCC optimize("-falign-functions")
#pragma GCC optimize("-fcse-skip-blocks")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
#pragma GCC optimize("no-stack-protector")
#pragma GCC optimize("-freorder-functions")
#pragma GCC optimize("-findirect-inlining")
#pragma GCC optimize("-fhoist-adjacent-loads")
#pragma GCC optimize("-frerun-cse-after-loop")
#pragma GCC optimize("inline-small-functions")
#pragma GCC optimize("-finline-small-functions")
#pragma GCC optimize("-ftree-switch-conversion")
#pragma GCC optimize("-foptimize-sibling-calls")
#pragma GCC optimize("-fexpensive-optimizations")
#pragma GCC optimize("-funsafe-loop-optimizations")
#pragma GCC optimize("inline-functions-called-once")
#pragma GCC optimize("-fdelete-null-pointer-checks")
#include<bits/stdc++.h>
using namespace std;
const int maxn=500005;
struct node{
int ls,rs;
int num;
long long sum;
}tree[21*maxn];
int mx;
int a[maxn];
int cnt;
int root[maxn];
inline int read(){
register int x=0,y=1;
register char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
return x*y;
}
inline void write(long long x){
if(!x)return ;
write(x/10);
putchar(x%10+'0');
return ;
}
inline void modify(register int x,register int y,register int l,register int r,register int p){
if(l>p||r<p)return ;
if(l==r){
tree[x].ls=tree[x].rs=0;
tree[x].num=tree[y].num+1;
tree[x].sum=tree[y].sum+p;
return ;
}
register int mid=l+((r-l)>>1);
if(p<=mid){
tree[x].ls=++cnt;
tree[x].rs=tree[y].rs;
modify(tree[x].ls,tree[y].ls,l,mid,p);
}
else{
tree[x].rs=++cnt;
tree[x].ls=tree[y].ls;
modify(tree[x].rs,tree[y].rs,mid+1,r,p);
}
tree[x].num=tree[y].num+1;
tree[x].sum=tree[y].sum+p;
return ;
}
inline int query1(register int x,register int y,register int l,register int r,register int p,register int q){
if(l>q||r<p)return 0;
if(l>=p&&r<=q)return tree[y].num-tree[x].num;
register int mid=l+((r-l)>>1);
register int tmp1,tmp2;
tmp1=query1(tree[x].ls,tree[y].ls,l,mid,p,q);
tmp2=query1(tree[x].rs,tree[y].rs,mid+1,r,p,q);
return tmp1+tmp2;
}
inline long long query2(register int x,register int y,register int l,register int r,register int p,register int q){
if(l>q||r<p)return 0;
if(l>=p&&r<=q)return tree[y].sum-tree[x].sum;
register int mid=l+((r-l)>>1);
register long long tmp1=0,tmp2=0;
tmp1=query2(tree[x].ls,tree[y].ls,l,mid,p,q);
tmp2=query2(tree[x].rs,tree[y].rs,mid+1,r,p,q);
return tmp1+tmp2;
}
inline void search(register int l,register int r,register int x,register int y){
register long long lft=l,rght=r;
l-=2;r+=2;
while(l+1<r){
register long long mid=l+((r-l)>>1);
if(query1(root[x-1],root[y],1,mx,1,mid)<=mid-lft+1)
r=mid;
else
l=mid;
}
register long long tmp1=(lft+r)*(r-lft+1)/2;
register long long tmp2=(r+1+rght)*(rght-r)/2;
register long long ans1=query2(root[x-1],root[y],1,mx,1,r);
register long long ans2=query2(root[x-1],root[y],1,mx,r+1,mx);
write(tmp1-ans1+ans2-tmp2);
if(tmp1-ans1+ans2-tmp2==0)putchar('0');
putchar('\n');
return ;
}
int main(){
register int n,m;
n=read();m=read();
tree[0].ls=tree[0].rs=tree[0].num=tree[0].sum=0;
for(int i=1;i<=n;i++){a[i]=read();mx=max(mx,a[i]);}
for(register int i=1;i<=n;i++){
root[i]=++cnt;
modify(root[i],root[i-1],1,mx,a[i]);
}
for(register int i=1;i<=m;i++){
register int l,r,k;
l=read();r=read();k=read();
search(k,k+r-l,l,r);
}
return 0;
}
[FJOI2016]神秘数
一样是推结论

考虑暴力我们可以先把区间排一遍序
然后暴力扫一遍按照上面的方法即可得到答案
复杂度O(n * n *log(n))
显然这个复杂度不够优秀
我们考虑现在已有可以凑出[1,y]
那么我们想求出在a[l,r]范围内权值在[1,y+1]内的所有数的权值和
这时我们的区间可以拓展为[1,sum],sum为权值和
而上面的操作可以通过主席树实现
我们考虑证明如此操作的复杂度

故每一次询问复杂度可以在O(logn*logT),T为值域
#include<bits/stdc++.h>
using namespace std;
const int maxn=100005;
struct node{
int ls,rs;
int sum;
}tree[31*maxn];
int cnt;
int root[maxn];
int read(){
int x=0,y=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
return x*y;
}
void modify(int x,int y,int l,int r,int p){
if(l>p||r<p)return ;
if(l==r){
tree[x].ls=tree[x].rs=0;
tree[x].sum=tree[y].sum+p;
return ;
}
int mid=l+((r-l)>>1);
tree[x].sum=tree[y].sum+p;
if(p<=mid){
tree[x].ls=++cnt;
tree[x].rs=tree[y].rs;
modify(tree[x].ls,tree[y].ls,l,mid,p);
}
else{
tree[x].rs=++cnt;
tree[x].ls=tree[y].ls;
modify(tree[x].rs,tree[y].rs,mid+1,r,p);
}
return ;
}
int query(int x,int y,int l,int r,int p,int q){
if(l>q||r<p)return 0;
if(l>=p&&r<=q)return tree[y].sum-tree[x].sum;
int mid=l+((r-l)>>1);
int tmp1=query(tree[x].ls,tree[y].ls,l,mid,p,q);
int tmp2=query(tree[x].rs,tree[y].rs,mid+1,r,p,q);
return tmp1+tmp2;
}
int main(){
int n,m;
n=read();
for(int i=1;i<=n;i++){
int x;
x=read();
root[i]=++cnt;
modify(root[i],root[i-1],1,1000000000,x);
}
m=read();
for(int i=1;i<=m;i++){
int l,r;
l=read();r=read();
int y=0,tmp;
while(1){
tmp=query(root[l-1],root[r],1,1000000000,1,y+1);
if(tmp>y)y=tmp;
else break;
}
printf("%d\n",y+1);
}
return 0;
}
另外,有一些主席树的经典应用
如维护一个二维矩阵的信息
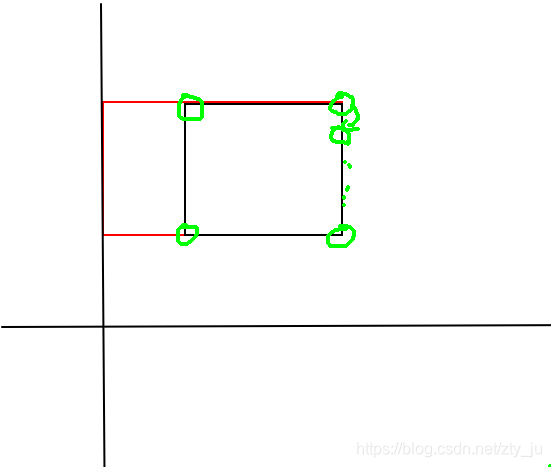
一样利用前缀的思想
