线段树合并
前置知识:权值线段树,动态开点线段树
学完也可以顺便把主席树学了
[Vani有约会]雨天的尾巴 /【模板】线段树合并
这是一道模板题,但首先得接触过树上差分。。
不会的建议学一下,不是什么很复杂的东西
我们知道,我们的点差分需要在路径的两端点加,lca减,lca的父亲减
但是这里有类型的限制,相同的类型才叠加在一起
我们对每一个树上的节点建一颗动态开点的权值线段树,权值表类型,里面记录类型个数
不然你空间没了
动态开点可以接受的原因是我们没插进一个值最多改变一颗线段树log个节点
那么由于我们做了树上差分,我们需要把子节点的信息传递给父节点
这里我们需要把子节点的线段树加到父结点的线段树上
那么这就需要线段树合并
核心做法
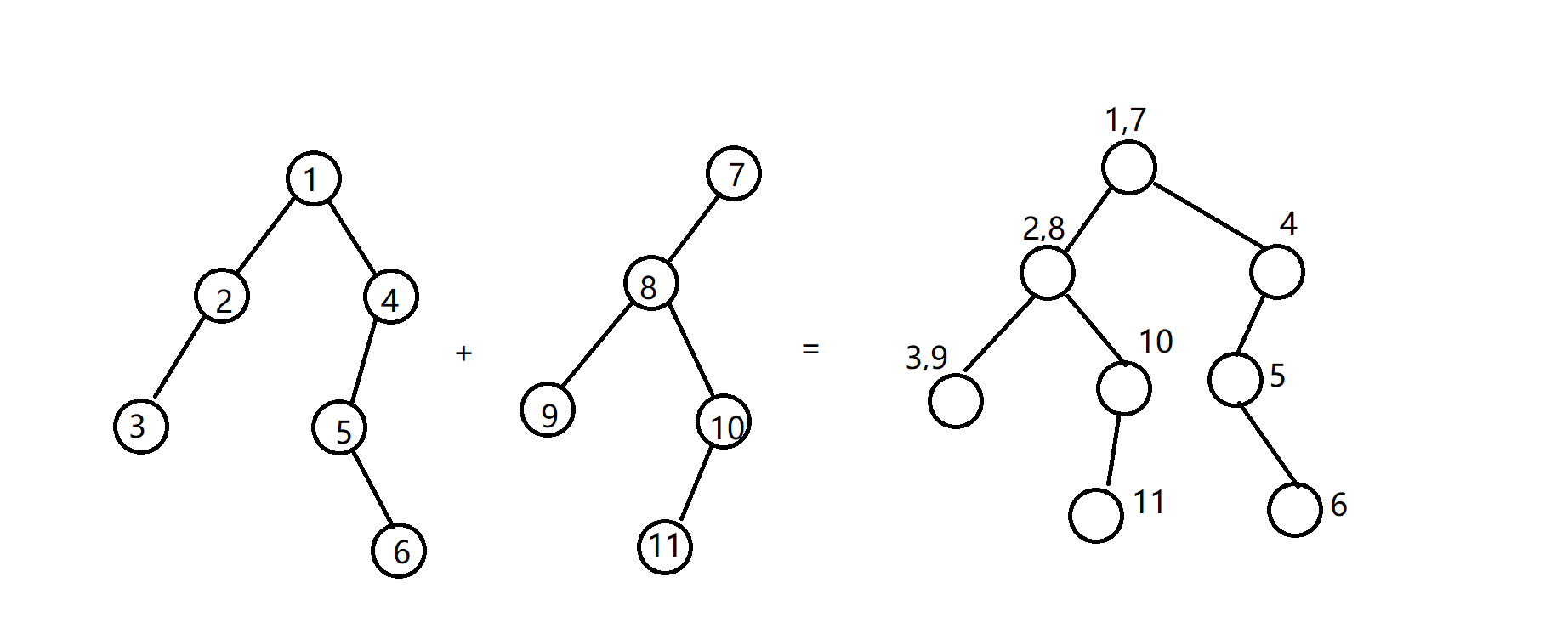
上图中的第一颗线段树与第二颗线段树的合并用了一个”+“表示
而数字表示每一个节点所维护的信息
得到的合并后的线段树的节点中有维护原树两个点信息的,都是我们需要遍历的点
而只维护了一个点信息的,代表某一棵树在这个位置没有节点即没有信息
我们直接指向另一个子节点即可(如果有接触过主席树这里应该很好理解)
int merge(int x,int y,int l,int r){
if(x==0||y==0)return x+y;//代表某棵待合并的线段树这个位置无信息
if(l==r){tree[x].mx+=tree[y].mx;return x;}//回溯
int mid=l+((r-l)>>1);
tree[x].ls=merge(tree[x].ls,tree[y].ls,l,mid);
tree[x].rs=merge(tree[x].rs,tree[y].rs,mid+1,r);
//这里和回溯的时候对于此题不需要新建节点,因为每棵线段树只用这一次就行
pushup(x);//更新节点数据
return x;
}
这是这个题的合并(merge)函数
而一般的题可能要在合并的过程中新建节点
时间复杂度分析
感谢hzr大佬的分享
本题对于每一条路径我们都可能增加最多4*logw个节点,w为类型的大小
则线段树(森林?)一共可能有mlogw个节点
对于加点显然是O(mlogw)的
而对于合并,我的dfs长这样
void dfs2(int x,int fa){
for(int i=head[x];i!=-1;i=e[i].nxt){
int tmp=e[i].to;
if(tmp==fa)continue;
dfs2(tmp,x);
rt[x]=merge(rt[x],rt[tmp],1,p);
}
ANS[x]=tree[rt[x]].ans;
if(tree[rt[x]].mx==0)ANS[x]=0;
return ;
}
即每次合并自己的所有子节点
我们计算merge里的遍历次数
我们把父节点与子节点的合并的遍历计算在子节点上
那么每一颗线段树最多被遍历一次
可能有人会对merge中的第一行的复杂度有疑问
注意,这里并没有对下面的子树继续遍历,而是直接返回
一共mlogw个节点,故复杂度O(mlogw)
#include<bits/stdc++.h>
using namespace std;
const int maxn=100005,maxm=100005,inf=0x3f3f3f3f;
struct node{
int ls,rs;
int mx,ans;
}tree[80*maxn];
int tot;
int rt[maxn];
struct upd{
int u,v,w,z;
bool operator <(upd i)const{
return w<i.w;
}
}a[maxm];
struct Edge{
int to,nxt;
}e[2*maxn];
int cnt;
int head[maxn];
int p=0;
int dep[maxn];
int f[maxn][21];
int val[maxm];
int ANS[maxn];
int read(){
int x=0,y=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
return x*y;
}
void add(int u,int v){
e[cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt++;
return ;
}
void dfs1(int x,int fa){
dep[x]=dep[fa]+1;
f[x][0]=fa;
for(int i=1;i<=20;i++)
f[x][i]=f[f[x][i-1]][i-1];
for(int i=head[x];i!=-1;i=e[i].nxt){
int tmp=e[i].to;
if(tmp==fa)continue;
dfs1(tmp,x);
}
return ;
}
int lca(int x,int y){
if(dep[x]<dep[y])swap(x,y);
for(int i=20;i>=0;i--)
if(dep[f[x][i]]>=dep[y])
x=f[x][i];
if(x==y)return x;
for(int i=20;i>=0;i--)
if(f[x][i]!=f[y][i]){
x=f[x][i];
y=f[y][i];
}
return f[x][0];
}
int newnode(){
tot++;
tree[tot].ls=tree[tot].rs=0;
tree[tot].mx=tree[tot].ans=0;
return tot;
}
void pushup(int k){
int ls=tree[k].ls,rs=tree[k].rs;
tree[k].mx=max(tree[ls].mx,tree[rs].mx);
if(tree[k].mx==0)
tree[k].ans=0;
else if(tree[k].mx==tree[ls].mx)
tree[k].ans=tree[ls].ans;
else
tree[k].ans=tree[rs].ans;
return ;
}
void modify(int &k,int l,int r,int p,int val){
if(!k)k=newnode();
if(l==r){tree[k].mx+=val;tree[k].ans=p;return ;}
int mid=l+((r-l)>>1);
if(p<=mid)modify(tree[k].ls,l,mid,p,val);
else modify(tree[k].rs,mid+1,r,p,val);
pushup(k);
return ;
}
int merge(int x,int y,int l,int r){
if(x==0||y==0)return x+y;
if(l==r){tree[x].mx+=tree[y].mx;return x;}
int mid=l+((r-l)>>1);
tree[x].ls=merge(tree[x].ls,tree[y].ls,l,mid);
tree[x].rs=merge(tree[x].rs,tree[y].rs,mid+1,r);
pushup(x);
return x;
}
void dfs2(int x,int fa){
for(int i=head[x];i!=-1;i=e[i].nxt){
int tmp=e[i].to;
if(tmp==fa)continue;
dfs2(tmp,x);
rt[x]=merge(rt[x],rt[tmp],1,p);
}
ANS[x]=tree[rt[x]].ans;
if(tree[rt[x]].mx==0)ANS[x]=0;
return ;
}
int main(){
int n,m;
n=read();m=read();
memset(head,-1,sizeof(head));
for(int i=1;i<n;i++){
int u,v;
u=read();v=read();
add(u,v);
add(v,u);
}
dfs1(1,0);
for(int i=1;i<=m;i++){
a[i].u=read();
a[i].v=read();
a[i].w=read();
}
sort(a+1,a+m+1);
a[0].w=0;
for(int i=1;i<=m;i++){
if(a[i].w>a[i-1].w)p++;
a[i].z=p;
val[p]=a[i].w;
}
tree[0].mx=0;tree[0].ans=0;
for(int i=1;i<=m;i++){
int LCA=lca(a[i].u,a[i].v);
modify(rt[a[i].u],1,p,a[i].z,1);
modify(rt[a[i].v],1,p,a[i].z,1);
modify(rt[LCA],1,p,a[i].z,-1);
if(f[LCA][0])modify(rt[f[LCA][0]],1,p,a[i].z,-1);
}
dfs2(1,0);
for(int i=1;i<=n;i++)
printf("%d\n",val[ANS[i]]);
return 0;
}
例题[HNOI2012]永无乡
一句话题意:无向图内动态加边,询问某个点所在连通块内的权值第k小
我们可以用并查集判断每一个点在哪一个连通块里
对于每一个连通块建一颗权值线段树可以在O(logn)的时间内得到区间的权值第k小
当两个连通块合并时,我们用线段树合并将两颗线段树合并起来
这里我们可以把并查集的合并过程建立出一棵树
我们的线段树合并相当于从叶子节点往上一步一步合并到根节点,复杂度和模板题一样
#include<bits/stdc++.h>
using namespace std;
const int maxn=100005;
struct node{
int ls,rs;
int num;
}t[20*maxn];
int tot;
int rt[maxn];
int f[maxn];
int val[maxn];
int read(){
int x=0,y=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
return x*y;
}
int find(int x){
if(f[x]==x)return x;
return f[x]=find(f[x]);
}
int newnode(){
tot++;
t[tot].ls=t[tot].rs=0;
t[tot].num=0;
return tot;
}
void pushup(int k){
t[k].num=t[t[k].ls].num+t[t[k].rs].num;
return ;
}
void modify(int &k,int l,int r,int p){
if(!k)k=newnode();
if(l==r){t[k].num++;return ;}
int mid=l+((r-l)>>1);
if(p<=mid)modify(t[k].ls,l,mid,p);
else modify(t[k].rs,mid+1,r,p);
pushup(k);
return ;
}
int merge(int x,int y,int l,int r){
if(x==0||y==0)return x+y;
if(l==r){t[x].num+=t[y].num;return x;}
int mid=l+((r-l)>>1);
t[x].ls=merge(t[x].ls,t[y].ls,l,mid);
t[x].rs=merge(t[x].rs,t[y].rs,mid+1,r);
pushup(x);
return x;
}
int query(int k,int l,int r,int p){
if(t[k].num<p)return -1;
if(l==r)return val[l];
int mid=l+((r-l)>>1);
int ls=t[k].ls,rs=t[k].rs;
if(t[ls].num>=p)return query(ls,l,mid,p);
return query(rs,mid+1,r,p-t[ls].num);
}
int main(){
int n,m,q;
n=read();m=read();
for(int i=1;i<=n;i++){
int rk;
rk=read();
val[rk]=i;
f[i]=i;
modify(rt[i],1,n,rk);
}
for(int i=1;i<=m;i++){
int u,v;
u=find(read());v=find(read());
if(u==v)continue;
f[v]=u;
rt[u]=merge(rt[u],rt[v],1,n);
}
q=read();
for(int i=1;i<=q;i++){
char opt;
int x,y;
cin>>opt;
x=find(read());y=read();
if(opt=='Q')printf("%d\n",query(rt[x],1,n,y));
else{
y=find(y);
if(x==y)continue;
f[y]=x;
rt[x]=merge(rt[x],rt[y],1,n);
}
}
return 0;
}
[POI2011]ROT-Tree Rotations
对于一个节点i,我们可以交换它的两个子树
而对于节点i的操作,只能影响到左(右)边边整体对右(左)边整体的逆序对贡献
也就是说,我们假如知道右边有哪些权值和左边有那些权值,对交换子树前后算一下贡献
判断出对于这个节点i该不该交换子树即可
想知道一颗子树的权值情况我们可以用一颗权值线段树来表示
在线段树合并时计算交换或不交换两种情况的贡献就可以了
#include<bits/stdc++.h>
using namespace std;
const int maxn=200005;
struct seg{
int ls,rs;
long long num;
}t[20*2*maxn];
int tot;
int rt[2*maxn];
struct Edge{
int to,nxt;
}e[2*maxn];
int cnt;
int head[2*maxn];
int n,m;
long long ans;
int read(){
int x=0,y=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
return x*y;
}
int newnode(){
tot++;
t[tot].ls=t[tot].rs=t[tot].num=0;
return tot;
}
void pushup(int k){
t[k].num=t[t[k].ls].num+t[t[k].rs].num;
return ;
}
void modify(int &k,int l,int r,int val){
if(!k)k=newnode();
if(l==r){t[k].num++;return ;}
int mid=l+((r-l)>>1);
if(val<=mid)modify(t[k].ls,l,mid,val);
else modify(t[k].rs,mid+1,r,val);
pushup(k);
return ;
}
int merge(int x,int y,int l,int r,long long &tmp1,long long &tmp2){
if(x==0||y==0)return x+y;
if(l==r){t[x].num+=t[y].num;return x;}
int mid=l+((r-l)>>1);
tmp1+=t[t[y].rs].num*t[t[x].ls].num;
tmp2+=t[t[x].rs].num*t[t[y].ls].num;
t[x].ls=merge(t[x].ls,t[y].ls,l,mid,tmp1,tmp2);
t[x].rs=merge(t[x].rs,t[y].rs,mid+1,r,tmp1,tmp2);
pushup(x);
return x;
}
void add(int u,int v){
e[cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt++;
return ;
}
void build_tree(){
int u=++m;
int k;
k=read();
if(!k){
add(u,m+1);
build_tree();
add(u,m+1);
build_tree();
}
else
modify(rt[u],1,n,k);
return ;
}
void dfs(int x){
long long tmp1=0,tmp2=0;
for(int i=head[x];i!=-1;i=e[i].nxt){
int tmp=e[i].to;
dfs(tmp);
rt[x]=merge(rt[x],rt[tmp],1,n,tmp1,tmp2);
}
ans+=min(tmp1,tmp2);
return ;
}
int main(){
n=read();
memset(head,-1,sizeof(head));
t[0].ls=t[0].rs=t[0].num=0;
build_tree();
dfs(1);
printf("%lld",ans);
return 0;
}
