前置知识
cdq分治,单调栈,二分
定义一个点的贡献为以该点为右上角的合法矩形个数
我们先考虑固定矩形的右上端点i
那么能和该右上端点i组成合法矩形的一定是下图这样的
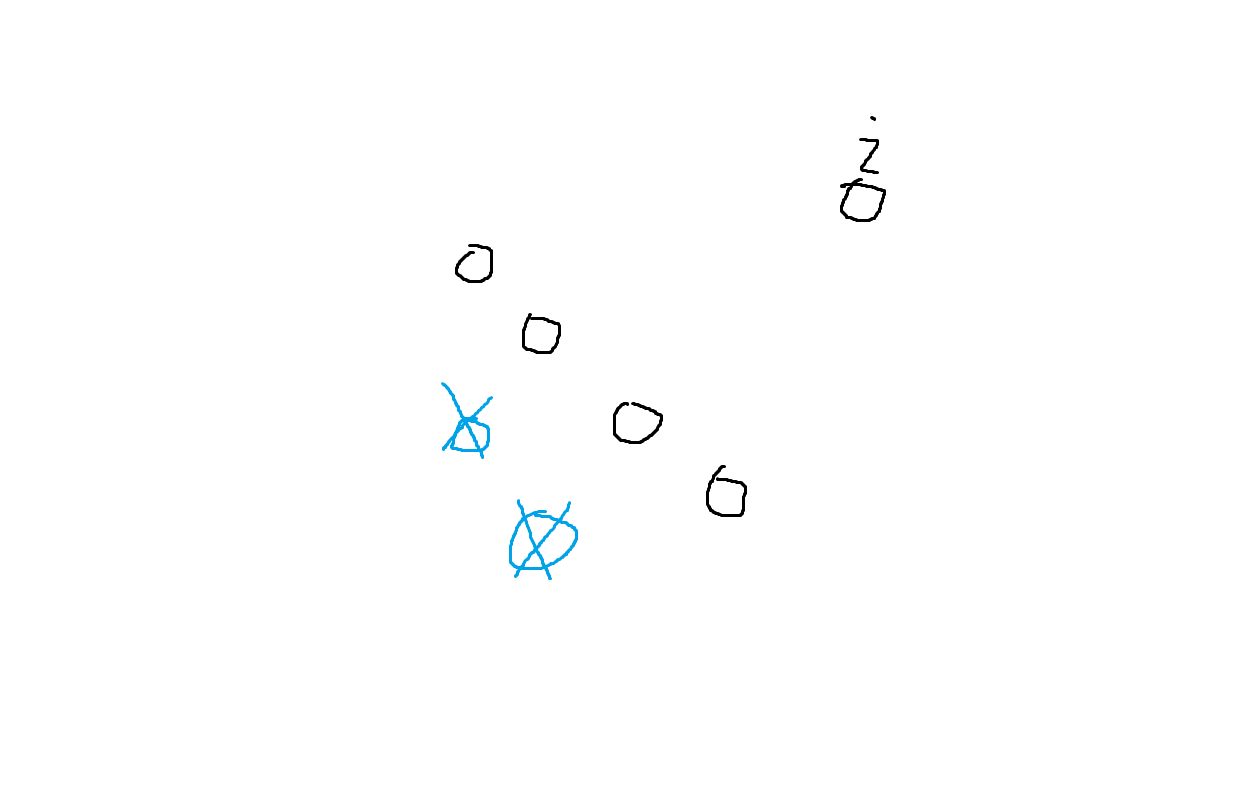
黑点是合法的,蓝点是非法的
对i有贡献的点一定是x递减y递增的
我们可以把这个东西用一个单调栈来维护
记该单调栈为s1
对于一堆的右上端点,我们考虑维护一个x递增,y递增的单调栈s2
那么当一个点加进单调栈中时,可能会pop掉一些点
操作完后该点的答案应该是我们维护的s1中所有y值大于等于s2中的第二个点的y值且小于等于该点y值的点数
这个可以二分一下得到
这一步的原因是会被s2中的第二个点挡住一部分s1中的点,如下图
黑点为s2中的点,蓝点为s1中的点
红色区域的蓝点是无法给右上角黑点贡献的
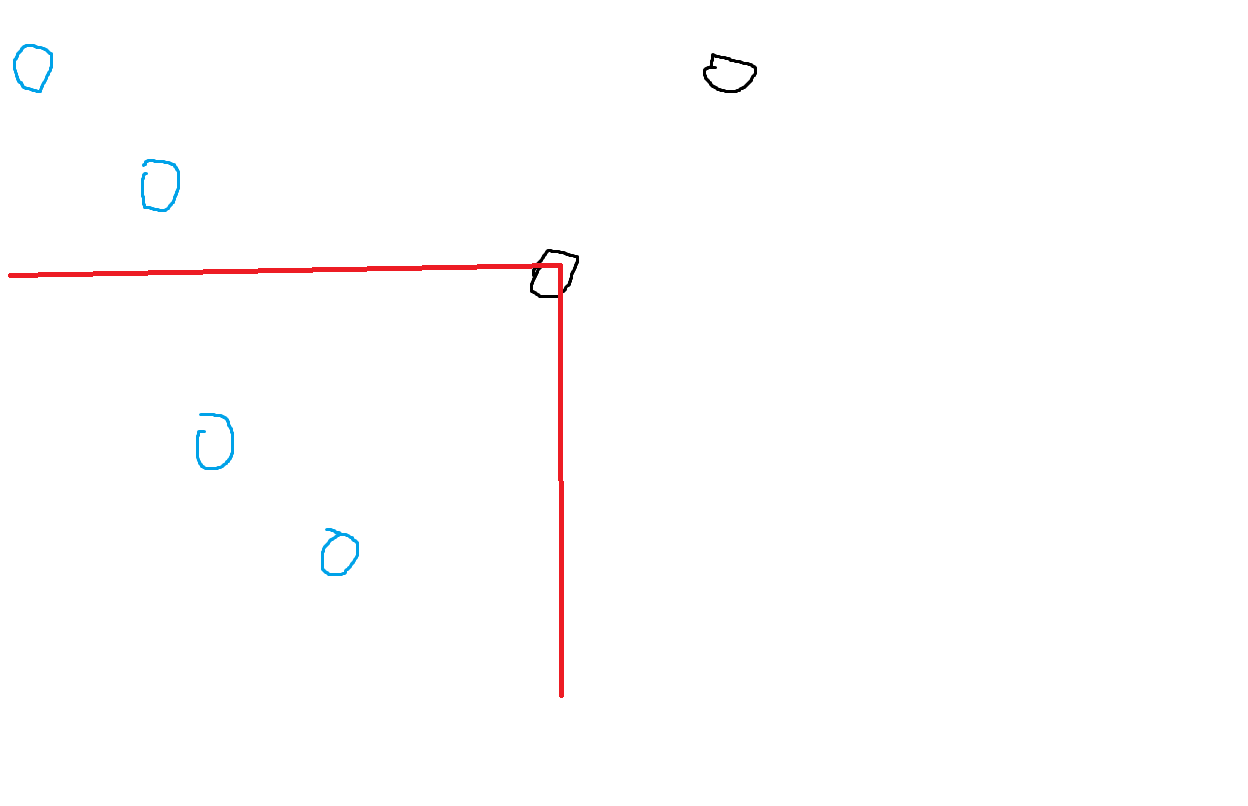
总答案即每个点答案之和
但这个根本没法直接维护,我们考虑cdq分治
将所有点按x从小到大排序,进cdq分治,对y归并排序
每一层只计算左半边的点对右半边的点产生的贡献
在归并y的同时,维护s1和s2
方法如上述
由于对于每一个i点,所有x小于的点都会在cdq中被考虑是否对i有贡献,故计算的答案是不重不漏的
#include<bits/stdc++.h>
using namespace std;
const int maxn=200005;
struct point{
int x,y;
}a[maxn],b[maxn],st1[maxn],st2[maxn];
long long ANS=0;
int read(){
int x=0,y=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
return x*y;
}
bool cmp(point p,point q){
return p.x<q.x;
}
long long search(int tp,int y){
int l=0,r=tp+1;
while(l+1<r){
int mid=l+((r-l)>>1);
if(st1[mid].y>=y)
r=mid;
else
l=mid;
}
return tp-r+1;
}
void merge_sort(int l,int r){
int mid=l+((r-l)>>1);
int p=l,q=mid+1,len=l,tp1=0,tp2=0;
while(p<=mid&&q<=r){
if(a[p].y<=a[q].y){
while(tp1>=1&&st1[tp1].x<a[p].x)tp1--;
st1[++tp1]=a[p];
b[len++]=a[p++];
}
else{
while(tp2>=1&&st2[tp2].x>a[q].x)tp2--;
st2[++tp2]=a[q];
ANS+=search(tp1,st2[tp2-1].y);
b[len++]=a[q++];
}
}
while(p<=mid)b[len++]=a[p++];
while(q<=r){
while(tp2>=1&&st2[tp2].x>a[q].x)tp2--;
st2[++tp2]=a[q];
ANS+=search(tp1,st2[tp2-1].y);
b[len++]=a[q++];
}
for(int i=l;i<=r;i++)a[i]=b[i];
return ;
}
void cdq(int l,int r){
if(l==r)return ;
int mid=l+((r-l)>>1);
cdq(l,mid);
cdq(mid+1,r);
merge_sort(l,r);
return ;
}
int main(){
int n;
n=read();
for(int i=1;i<=n;i++){
a[i].x=read();
a[i].y=read();
}
sort(a+1,a+n+1,cmp);
cdq(1,n);
printf("%lld\n",ANS);
return 0;
}
