莫队

莫队是啥？

是莫涛队长提出的一个离线处理区间问题的暴力毒瘤算法

算法思想基于分块

普通莫队

【模板】莫队

莫队算法操作如下

我们考虑有两个指针l,r

表示我们现在维护的数据是[l,r]这个区间内的数据

我们想要O(1)的做到将这个区间转移到[l,r-1],[l,r+1],[l-1,r],[l+1,r]

然后通过离线，将查询神奇的排序，以达到我们可以承受的复杂度

我们不排序直接让l,r两个指针按原本的输入顺序去移动的话

时间复杂度达到O(nm),n为序列长度，m为查询次数

我们考虑分块

具体排序如下

struct query{
    int id;//原输入顺序
	int x,y;//左右边界
    bool operator <(query i)const{
		return x/block==i.x/block?y<i.y?x<i.x
	}
}

block为我们的分块大小

也就是说当两个询问的左边界在同一个块里时保证有边界递增

若左边界不在同一个块里，保证左边界递增

复杂度分析：

设块大小为B

块数量则为n/B

我们考虑分别计算l和r的移动

1. l在同一个块内

那么此时r一定是递增的对于每一个快最坏情况下都是O(n)级别

总复杂度O(n/b*n)

考虑l在块内最多移动O(B),最坏情况下所有询问的l在同一个块的左右两边

总复杂度O(m*B)

2. l不在同一个块内

那么此时r一定是放飞自我的，对于每一次这样的情况2都是O(n)

又因为跨块的l最多出现n/B次

总复杂度O(n/B*n)

考虑l最坏移动O(2*B)也就是O(B)级别，总共n/B次这样的移动

总复杂度O(B*n/B)

将上述的复杂度加起来

应该是O(n^2/B+ m*B)这个级别的

我们考虑尽量优秀的复杂度B可以选择sqrt(n)这样的块大小

复杂度O(n*sqrt(n))

当然块大小调成根号n并不一定是最优的情况

你也有可能碰到块大小根号死都过不去的情况

毕竟刚才的一波分析是基于最坏最坏的情况考虑的

如果更加详尽的考虑情况之间的关系，能得到一个更加优秀的块大小

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=50005,maxm=50005;
struct query{
	int id;
	int l,r;
}q[maxm];
int a[maxn];
int b[maxn];
int cnt[maxn];
long long k[maxm];
long long ans[maxm];
long long tmp=0;
bool flag[maxm];
bool cmp(query i,query j){
	return b[i.l]==b[j.l]?i.r<j.r:i.l<j.l;
}
void ins(int x){
	tmp+=2*cnt[a[x]];
	cnt[a[x]]++;
	return ;
}
void del(int x){
	tmp-=2*cnt[a[x]]-2;
	cnt[a[x]]--;
	return ;
}
long long gcd(long long a,long long b){
	return b==0?a:gcd(b,a%b);
}
signed main()
{
	int n,m;
	scanf("%lld%lld",&n,&m);
	for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
	int p=sqrt(n);
	for(int i=1;i<=n;i++){
		b[i]=i/p+1;
		if(i%p==0)b[i]--;
	}
	for(int i=1;i<=m;i++){
		int l,r;
		scanf("%lld%lld",&l,&r);
		q[i].l=l;q[i].r=r;
		q[i].id=i;
	}
	sort(q+1,q+m+1,cmp);
	int l=1,r=0;
	for(int i=1;i<=m;i++){
		int ql=q[i].l,qr=q[i].r;
		while(l>ql)ins(--l);
		while(l<ql)del(l++);
		while(r>qr)del(r--);
		while(r<qr)ins(++r);
		ans[q[i].id]=tmp;
		k[q[i].id]=(q[i].r-q[i].l+1)*(q[i].r-q[i].l);
		if(q[i].l==q[i].r)
			flag[q[i].id]=1;
	}
	for(int i=1;i<=m;i++){
		if(flag[i]){printf("0/1\n");continue;}
		long long g=gcd(ans[i],k[i]);
		printf("%lld/%lld\n",ans[i]/g,k[i]/g);
	}
	return 0;
}

这份代码是刚开始学莫队时写的

可以考虑看看接下来莫队例题的代码

[SDOI2009]HH的项链

这道题好像莫队过不去qaq

但确实是一道比上面那道题还模板的莫队题

只要用cnt数组记录下每个颜色的出现次数

ins的时候若cnt从0变1就ans++

del的时候若cnt从1变0就ans--

模板题

小B的询问

好像和小z的袜子区别不大

维护出现次数的平方和

若原某数字出现次数为x

现在变成了x+val

$(x+val)^2=x^2+2*x*val+val^2\\ 也就是说对于x^2，我们加上2*x*val+val^2就变成(x+val)^2了$

#include<bits/stdc++.h>
using namespace std;
const int maxn=50005,maxm=50005,maxk=50005;
struct query{
	int id;
	int l,r;
}q[maxm];
int a[maxn];
int b[maxn];
int cnt[maxk];
long long ans[maxm];
long long tmp=0;
bool cmp(query i,query j){
	return b[i.l]==b[j.l]?i.r<j.r:i.l<j.l;
}
void ins(int x){
	tmp+=2*cnt[a[x]]+1;
	cnt[a[x]]++;
	return ;
}
void del(int x){
	tmp-=2*cnt[a[x]]-1;
	cnt[a[x]]--;
}
int main()
{
	int n,m,k;
	scanf("%d%d%d",&n,&m,&k);
	for(int i=1;i<=n;i++)scanf("%d",&a[i]);
	int p=sqrt(n);
	for(int i=1;i<=n;i++){
		b[i]=i/p+1;
		if(i%p==0)b[i]--;
	}
	for(int i=1;i<=m;i++){
		int l,r;
		scanf("%d%d",&l,&r);
		q[i].l=l;q[i].r=r;
		q[i].id=i;
	}
	sort(q+1,q+m+1,cmp);
	int l=1,r=0;
	for(int i=1;i<=m;i++){
		int ql=q[i].l,qr=q[i].r;
		while(l>ql)ins(--l);
		while(l<ql)del(l++);
		while(r>qr)del(r--);
		while(r<qr)ins(++r);
		ans[q[i].id]=tmp;
	}
	for(int i=1;i<=m;i++)
		printf("%lld\n",ans[i]);
	return 0;
}

[CQOI2018]异或序列

CF617E双倍经验

$显然我们可以把a_x\bigoplus a_{x+1}\bigoplus...\bigoplus a_y变成\\ b_y\bigoplus b_{x-1}，其中b_i=a_1\bigoplus a_2\bigoplus...\bigoplus a_i\\ 也就是找在[l,r]内有多少对点满足上述条件\\ 我们在ins一个位置进来时，只需考虑原本的区间里的数和ins进来的数是否能异或得到k\\ 我们考虑还是要cnt数组，cnt_x意义为编号为值为x的b有多少个\\ 那么能和我们ins进来的b_i配对变成k的当然就是那些b值为k\bigoplus b_i的\\ del的话基本同理\\ 注意一下顺序$

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=100005,maxm=100005,maxc=1<<21;
int base;
struct query{
	int id;
	int x,y;
	bool operator <(query i)const{
		return x/base==i.x/base?y<i.y:x<i.x;
	}
}q[maxm];
int n,m,k;
int ans;
int a[maxn];
int cnt[maxc];
int ANS[maxm];
inline int read(){
	register int x=0,y=1;
	register char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
	while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	return x*y;
}
inline void write(register int x){
	if(!x)return ;
	write(x/10);
	putchar(x%10+'0');
	return ;
}
inline void ins(register int x){
    ans+=cnt[a[x]^k];
	cnt[a[x]]++;
	return ;
}
inline void del(register int x){
	cnt[a[x]]--;
	ans-=cnt[a[x]^k];
	return ;
}
signed main(){
	n=read();m=read();k=read(); 
	base=sqrt(n);
	for(register int i=1;i<=n;i++)a[i]=a[i-1]^read();
	for(register int i=1;i<=m;i++){
		register int l,r;
		l=read();r=read();
		q[i].id=i;
		q[i].x=l;
		q[i].y=r;
	}
	sort(q+1,q+m+1);
	register int l=1,r=0;
	for(register int i=1;i<=m;i++){
		register int id=q[i].id,x=q[i].x-1,y=q[i].y;
		while(l<x)del(l++);
		while(l>x)ins(--l);
		while(r<y)ins(++r);
		while(r>y)del(r--);
		ANS[id]=ans;
	}
	for(register int i=1;i<=m;i++){
		write(ANS[i]);
		if(!ANS[i])putchar('0');
		putchar('\n');
	}
	return 0;
}

美好的每一天

注意到回文串只可能是所有字母都是偶数个或者仅有一个字母是奇数个

由于区间内我们只关心字母的奇偶，想到异或

对于一个区间我们用一个26位的二进制数表示每一个字母出现次数为奇或偶(0偶1奇)

而我们只要把所有的前缀区间的状态计算出来，对于任意一个区间我们都可以异或得到答案

定义a_i表示区间[1,i]的各个字母出现状态的值

[x,y]的状态即

$a_y\bigoplus a_{x-1}$

那么其实原问题就被我们转换成对于一个区间[x,y]

选择i属于[x-1,y]的两个不同位置的a值进行异或是否能得到0或者2的某次方

得到0即字母都是奇数个，2的某次方即仅有一个字母是奇数个

我们考虑莫队区间拓展的过程

进来一个值时相当于多了一个a值x可用

根据异或的传递性，我们查询原本这个区间里a值等于x的有多少和a值等于x异或2的某次方的有多少

删除同理

复杂度

$O(26*n\sqrt n)$

#include<bits/stdc++.h>
using namespace std;
const int maxn=60005,maxm=60005;
int n,m;
int base;
struct query{
	int id;
	int x,y;
	bool operator <(query i)const{
		return x/base==i.x/base?y<i.y:x<i.x;
	}
}q[maxm];
int ans=0;
int a[maxn];
int cnt[(1<<26)+5];
int ANS[maxm];
inline int read(){
	register int x=0,y=1;
	register char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
	while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	return x*y;
}
inline void ins(register int x){
	ans+=cnt[a[x]];
	cnt[a[x]]++;
	for(register int i=0;i<26;i++)
		ans+=cnt[a[x]^(1<<i)];
	return ;
}
inline void del(register int x){
	cnt[a[x]]--;
	ans-=cnt[a[x]];
	for(register int i=0;i<26;i++)
		ans-=cnt[a[x]^(1<<i)];
	return ;
}
int main(){
	n=read();m=read();
	base=3*sqrt(n);
	for(register int i=1;i<=n;i++){
		register char c;
		cin>>c;
		a[i]=1<<(c-'a');
		a[i]^=a[i-1];
	}
	for(register int i=1;i<=m;i++){
		q[i].id=i;
		q[i].x=read();
		q[i].y=read();
	}
	sort(q+1,q+m+1);
	int l=1,r=0;
	for(register int i=1;i<=m;i++){
		register int x=q[i].x-1,y=q[i].y,id=q[i].id;
		while(l<x)del(l++);
		while(l>x)ins(--l);
		while(r>y)del(r--);
		while(r<y)ins(++r);
		ANS[id]=ans;
	}
	for(register int i=1;i<=m;i++)printf("%d\n",ANS[i]);
	return 0;
}

Chika and Friendly Pairs

我们想知道对于一个数a[i]有多少个数的值在[a[i]-k,a[i]+k]这个区间内

我们可以在莫队的时候做树状数组

复杂度

$O(n\times \sqrt n\times logn)$

#include<bits/stdc++.h>
using namespace std;
const int maxn=27005,maxm=27005;
int block;
struct Query{
    int id;
    int x,y;
    bool operator <(Query i)const{
        return x/block==i.x/block?y<i.y:x<i.x;
    }
}q[maxm];
struct node{
    int id,data;
    bool operator <(node i)const{
        return data<i.data;
    }
}a[maxn];
int n,m,k,w;
int ans=0;
int b[maxn];
int c[maxn];
int pos[maxn][2];
int ANS[maxm];
int tree[maxn];
inline int read(){
    register int x=0,y=1;
    register char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
    while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
    return x*y;
}
inline int lowbit(register int x){
    return x&-x;
}
inline void update(register int x,register int val){
    while(x<=w){
        tree[x]+=val;
        x+=lowbit(x);
    }
    return ;
}
inline int query(register int x){
    register int sum=0;
    while(x){
        sum+=tree[x];
        x-=lowbit(x);
    }
    return sum;
}
inline int search(int x){
    register int l=0,r=w+1;
    while(l+1<r){
        register int mid=l+((r-l)>>1);
        if(b[mid]<=x)
            l=mid;
        else
            r=mid;
    }
    return l;
}
inline void ins(register int x){
    register int pos1=pos[c[x]][0],pos2=pos[c[x]][1];
    register int tmp1=query(pos1),tmp2=query(pos2-1);
    ans+=tmp1-tmp2;
    update(c[x],1);
    return ;
}
inline void del(register int x){
    update(c[x],-1);
    register int pos1=pos[c[x]][0],pos2=pos[c[x]][1];
    register int tmp1=query(pos1),tmp2=query(pos2-1);
    ans-=tmp1-tmp2;
    return ;
}
signed main(){    
    n=read();m=read();k=read();
    block=pow(n,0.5);
    for(register int i=1;i<=n;i++){
        a[i].id=i;
        a[i].data=read();
    }
    sort(a+1,a+n+1);
    a[0].data=-1;
    for(register int i=1;i<=n;i++){
        if(a[i].data>a[i-1].data)b[++w]=a[i].data;
        c[a[i].id]=w;
    }
    for(int i=1;i<=w;i++){
        register int pos1=search(b[i]+k),pos2=search(b[i]-k);
        if(b[pos2]<b[i]-k)pos2++;
        if(pos2==0)pos2=1;
        pos[i][0]=pos1;pos[i][1]=pos2;
    }
    for(register int i=1;i<=m;i++){
        q[i].id=i;
        q[i].x=read();
        q[i].y=read();
    }
    sort(q+1,q+m+1);
    register int l=1,r=0;
    for(register int i=1;i<=m;i++){
        int id=q[i].id,x=q[i].x,y=q[i].y;
        while(l<x)del(l++);
        while(l>x)ins(--l);
        while(r<y)ins(++r);
        while(r>y)del(r--);
        ANS[id]=ans;
    }
    for(register int i=1;i<=m;i++)printf("%d\n",ANS[i]);
    return 0;
}

[Ynoi2016]这是我自己的发明

先看弱化版[Snoi2017]一个简单的询问

我们设

$f(l_1,r_1,l_2,r_2)为区间[l_1,r_1]和[l_2,r_2]中各取一个的权值相同情况总数\\ 但4元我们不好处理\\ 容斥\\ f(l_1,r_1,l_2,r_2)=f(1,r_1,1,r_2)-f(1,l_2-1,1,r_1)-f(1,l_1-1,1,r_2)+f(1,l_1-1,1,l_2-1)\\ 这样的话每一个f就只有两元了$

我们用图来形象的看一看这个容斥

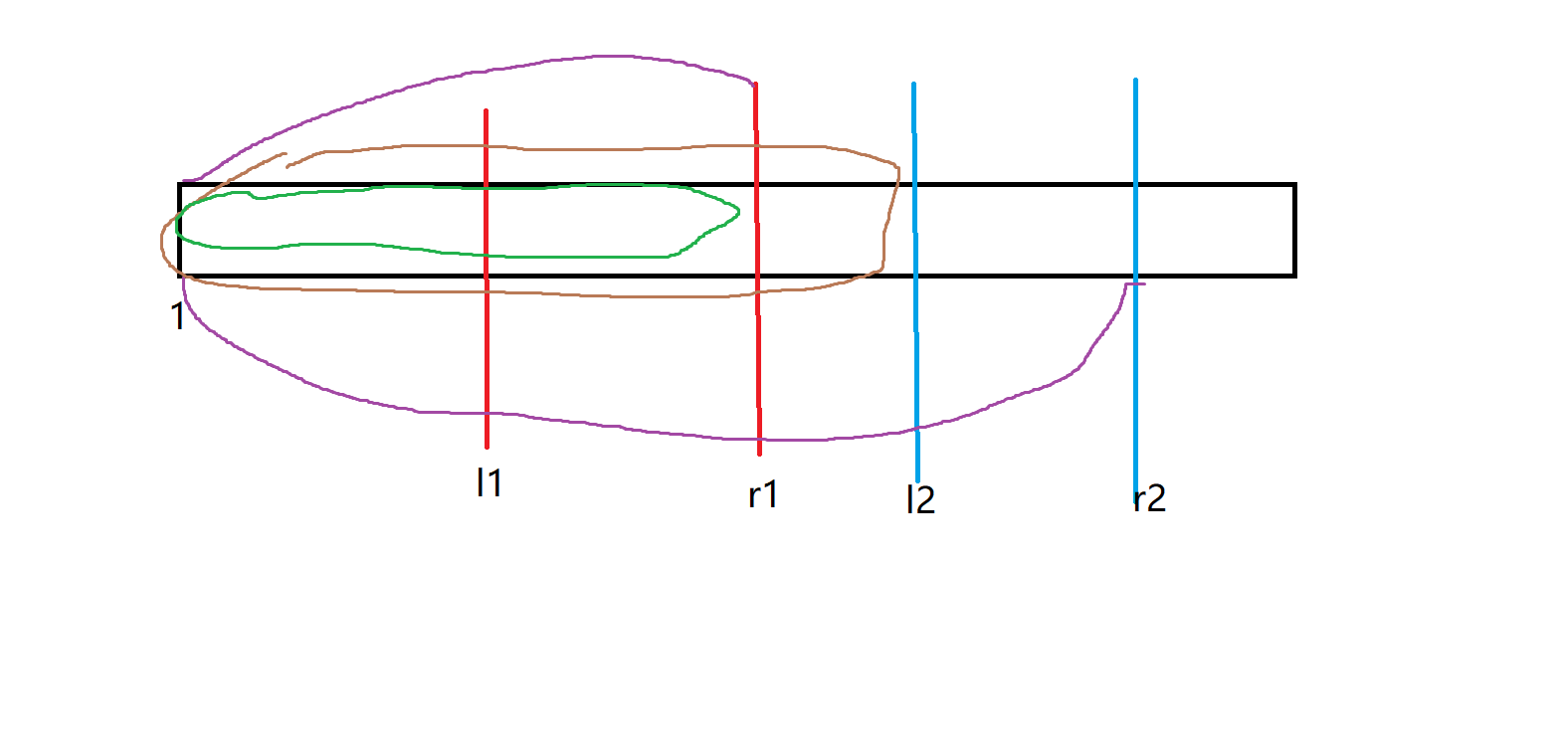
我们首先计算了两个紫色区间的f

那么，棕色区间([1,l2-1])和绿色区间([1,r1])的f是我们不应该计算的

同理[1,l1-1]和[1,r2]是我们不该计算的

两个均减去的话，把[1,l1-1]和[1,l2-1]的f减了两遍，加回来即可

然后对于区间1统计某数字个数的问题我们用普通莫队解决

我们发现我们需要计算的都是f(1,x,1,y)这个形式

不妨设x小于y

对于一个数字k，它对答案的贡献即[1,x]内k数量乘以[1,y]内k数量

设s1=[1,x]内k数量,s2=[1,y]内k数量

在莫队l指针向左时，某个k的s1应该减少1，所有s2不变，对答案贡献-s2

l指针向右，某个k的s1应该增加1，所有s2不变，对答案贡献s2

在莫队r指针向左时，某个k的s2应该减少1，所有s1不变，对答案贡献-s1

r指针向右，某个k的s2应该增加1，所有s1不变，对答案贡献s1

我们拿两个数组记录数量就好了

#include<bits/stdc++.h>
using namespace std;
const int maxn=50005,maxm=50005;
int block;
struct Query{
	int id,x,y;
	bool operator <(Query i)const{
		return ((x-1)/block==(i.x-1)/block)?y<i.y:x<i.x;
	}
}q[4*maxm];
int a[maxn];
long long ans=0;
int cnt1[maxn],cnt2[maxn];
long long ANS[maxm];
int read(){
	int x=0,y=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
	while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	return x*y;
}
void ins1(int x){
	ans+=cnt2[a[x]];
	cnt1[a[x]]++;
	return ;
}
void ins2(int x){
	ans+=cnt1[a[x]];
	cnt2[a[x]]++;
	return ;
}
void del1(int x){
	ans-=cnt2[a[x]];
	cnt1[a[x]]--;
	return ;
}
void del2(int x){
	ans-=cnt1[a[x]];
	cnt2[a[x]]--;
	return ;
}
int main(){
	int n,m,Q=0;
	n=read();
	block=sqrt(n);
	for(int i=1;i<=n;i++)a[i]=read();
	m=read();
	for(int i=1;i<=m;i++){
		int l1,r1,l2,r2;
		l1=read();r1=read();l2=read();r2=read();
		Q++;q[Q].id=i;q[Q].x=r1;q[Q].y=r2;
		if(q[Q].x>q[Q].y)swap(q[Q].x,q[Q].y);
		Q++;q[Q].id=-i;q[Q].x=l2-1;q[Q].y=r1;
		if(q[Q].x>q[Q].y)swap(q[Q].x,q[Q].y);
		Q++;q[Q].id=-i;q[Q].x=l1-1;q[Q].y=r2;
		if(q[Q].x>q[Q].y)swap(q[Q].x,q[Q].y);
		Q++;q[Q].id=i;q[Q].x=l1-1;q[Q].y=l2-1;
		if(q[Q].x>q[Q].y)swap(q[Q].x,q[Q].y);
	}
	sort(q+1,q+Q+1);
	int l=0,r=0;
	for(int i=1;i<=Q;i++){
		int id=q[i].id,x=q[i].x,y=q[i].y;
		while(l<x)ins2(++l);
		while(l>x)del2(l--);
		while(r<y)ins1(++r);
		while(r>y)del1(r--);
		ANS[abs(id)]+=(id<0?-ans:ans);
	}
	for(int i=1;i<=m;i++)printf("%lld\n",ANS[i]);
	return 0;
}

我们看到这一题

需要两种操作

换根和询问两颗子树内点权相等情况总数

我们考虑用一个dfs求出dfs序

我们知道一棵子树x的所有点在dfs序上的位置是[dfn[x],dfn[x]+son[x]-1]

dfn[x]是x的dfs序，son[x]是x的子树大小

而换根对于一个x只有两种情况

即根在x的子树里（指根为1时树的形态中）和不在

在时，不难发现，x的子树会变成所有节点除去x的某个儿子的子树

这个儿子是根往x走的最后一个节点

不在x子树里就什么也不会发生，x的子树还是x的子树

由于区间要么是某棵子树，要么是全部节点去掉某棵子树

我们把dfs序复制一遍粘后面

暴政一定能变成一个区间

然后就按弱化版的方法搞即可

#include<bits/stdc++.h>
using namespace std;
const int maxn=100005,maxm=500005;
int block;
struct Query{
	int id,x,y;
	bool operator <(Query i)const{
		return ((x-1)/block==(i.x-1)/block)?y<i.y:x<i.x;
	}
}q[4*maxm];
struct node{
	int id,val;
	bool operator <(node i)const{
		return val<i.val;
	}
}b[maxn];
struct Edge{
	int to;
	int nxt;
}e[2*maxn];
int cnt;
int head[maxn];
int dfsnum;
int a[maxn];
int c[2*maxn],dfn[maxn],son[maxn];
int dep[maxn],f[maxn][21];
long long ans=0;
int cnt1[maxn],cnt2[maxn];
long long ANS[maxm];
int read(){
	int x=0,y=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
	while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	return x*y;
}
void add(int u,int v){
	e[cnt].to=v;
	e[cnt].nxt=head[u];
	head[u]=cnt++;
	return ;
}
void dfs(int x,int fa){
	dfn[x]=++dfsnum;
	c[dfsnum]=x;
	son[x]=1;
	dep[x]=dep[fa]+1;
	f[x][0]=fa;
	for(int i=1;i<=20;i++)f[x][i]=f[f[x][i-1]][i-1];
	for(int i=head[x];i!=-1;i=e[i].nxt){
		int tmp=e[i].to;
		if(tmp==fa)continue;
		dfs(tmp,x);
		son[x]+=son[tmp];
	}
	return ;
}
int lca(int x,int y){
	if(dep[x]<dep[y])swap(x,y);
	for(int i=20;i>=0;i--)
		if(dep[f[x][i]]>=dep[y])
			x=f[x][i];
	if(x==y)return x;
	for(int i=20;i>=0;i--)
		if(f[x][i]!=f[y][i]){
			x=f[x][i];
			y=f[y][i];
		}
	return f[x][0];
}
int get(int x,int y){
	if(dep[x]<dep[y])swap(x,y);
	for(int i=20;i>=0;i--)
		if(dep[f[x][i]]>dep[y])
			x=f[x][i];
	return x;
}
void ins1(int x){
	ans+=cnt2[a[c[x]]];
	cnt1[a[c[x]]]++;
	return ;
}
void ins2(int x){
	ans+=cnt1[a[c[x]]];
	cnt2[a[c[x]]]++;
	return ;
}
void del1(int x){
	ans-=cnt2[a[c[x]]];
	cnt1[a[c[x]]]--;
	return ;
}
void del2(int x){
	ans-=cnt1[a[c[x]]];
	cnt2[a[c[x]]]--;
	return ;
}
int main(){
	int n,m,Q=0;
	n=read();m=read();
	block=sqrt(2*n);
	memset(head,-1,sizeof(head));
	for(int i=1;i<=n;i++){b[i].id=i;b[i].val=read();}
	sort(b+1,b+n+1);
	int w=0;
	b[0].val=0;
	for(int i=1;i<=n;i++){
		if(b[i].val>b[i-1].val)w++;
		a[b[i].id]=w;
	}
	for(int i=1;i<n;i++){
		int u,v;
		u=read();v=read();
		add(u,v);
		add(v,u);
	}
	dfs(1,0);
	for(int i=n+1;i<=2*n;i++)c[i]=c[i-n];
	int rt=1;
	for(int i=1;i<=m;i++){
		int opt,x,y;
		int l1,r1,l2,r2,u;
		opt=read();x=read();
		if(opt==1){rt=x;ANS[i]=-1;}
		else{
			y=read();
			if(rt==x)l1=1,r1=n;
			else if(lca(rt,x)!=x)l1=dfn[x],r1=dfn[x]+son[x]-1;
			else{
				u=get(rt,x);
				l1=dfn[u]+son[u];r1=n+dfn[u]-1;
			}
			if(rt==y)l2=1,r2=n;
			else if(lca(rt,y)!=y)l2=dfn[y],r2=dfn[y]+son[y]-1;
			else{
				u=get(rt,y);
				l2=dfn[u]+son[u];r2=n+dfn[u]-1;
			}
			Q++;q[Q].id=i;q[Q].x=r1;q[Q].y=r2;
			if(q[Q].x>q[Q].y)swap(q[Q].x,q[Q].y);
			Q++;q[Q].id=-i;q[Q].x=l2-1;q[Q].y=r1;
			if(q[Q].x>q[Q].y)swap(q[Q].x,q[Q].y);
			Q++;q[Q].id=-i;q[Q].x=l1-1;q[Q].y=r2;
			if(q[Q].x>q[Q].y)swap(q[Q].x,q[Q].y);
			Q++;q[Q].id=i;q[Q].x=l1-1;q[Q].y=l2-1;
			if(q[Q].x>q[Q].y)swap(q[Q].x,q[Q].y);
		}
	}
	sort(q+1,q+Q+1);
	int l=0,r=0;
	for(int i=1;i<=Q;i++){
		int id=q[i].id,x=q[i].x,y=q[i].y;
		while(l<x)ins2(++l);
		while(l>x)del2(l--);
		while(r<y)ins1(++r);
		while(r>y)del1(r--);
		ANS[abs(id)]+=(id<0?-ans:ans);
	}
	for(int i=1;i<=m;i++)
		if(ANS[i]>-1)
			printf("%lld\n",ANS[i]);
	return 0;
}

带修莫队

[国家集训队]数颜色 / 维护队列

带修改数颜色

我们可以把修改看作第三维

第几次修改对应的第三维就是几

我们从(x,y,z)变到(x,y,z+1)或(x,y,z-1)是简单的

具体操作参考change函数

然后三维排序就看x在不在一个块里，再看y在不在一个块里，最后令z升序

时间复杂度O(n^1.66)

高得令人发指

时间复杂度分析：

$设块大小为B，块数量为\frac n B\\ l：\\ 在一个块内每次最多移动B次,复杂度O(\frac n B*\frac n B*B)\\ 跨块时最多移动B次，复杂度O(\frac n B*B)\\ 总复杂度：O(n+\frac {n^2}B)\\ r:\\ 当l同块，r同块，共单次移动B次，共\frac n B*\frac n B 次，复杂度O(\frac {n^2}B)\\ 当l在同块里，r跨块，共\frac n B个块,r可能跨块\frac n B次，每次移动B，复杂度O(\frac {n^2}B)\\ 当l跨块时，r最多移动n次，共B次跨块,复杂度O(nB)\\ 总复杂度O(\frac {n^2}B+nB)\\ p:\\ 当l同块,r同块时，p此时单调递增，复杂度O(n)\\ 当l在同块，r换块时，p放飞自我，共\frac n B*\frac n B次，每次移动n次，复杂度O(\frac {n^3}{B^2})\\ 当l跨块，r放飞自我，p放飞自我，共\frac n B次，每次移动n次，复杂度O(\frac{n^2}B)\\ 总复杂度O(n+\frac {n^3}{B^2}+\frac{n^2}B)\\ 全加起来：\\ O(n+\frac {n^2}B+\frac {n^2}B+nB+n+\frac {n^3}{B^2}+\frac{n^2}B)\\ 忽略常数\\ O(n+nB+\frac {n^2}B+\frac {n^3}{B^2})\\ 设B=n^x\\ O(n+n^{1+x}+n^{2-x}+n^{3-2x})\\ 我们想使复杂度优让max(1+x,2-x,3-2x)最小即可\\ x=\frac 2 3,时间复杂度O(n^{\frac 5 3})$

#include<bits/stdc++.h>
using namespace std;
const int maxn=133338,maxm=133338;
int base;
struct query{
	int id;
	int x,y,t;
	bool operator <(query i)const{
		return x/base==i.x/base?(y/base==i.y/base?t<i.t:y<i.y):x<i.x;
	}
}q[maxm];
int c[maxn];
int a[maxm][2];
int l,r,p;
int ans=0;
int ANS[maxm];
int cnt[1000005];
bool vis[maxm];
inline int read(){
	register int x=0,y=1;
	register char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
	while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	return x*y;
}
inline void write(register int x){
	if(!x)return ;
	write(x/10);
	putchar(x%10+'0');
	return ;
}
inline void ins(register int x){
	cnt[c[x]]++;
	if(cnt[c[x]]==1)ans++;
	return ;
}
inline void del(register int x){
	cnt[c[x]]--;
	if(!cnt[c[x]])ans--;
	return ;
}
inline void change(register int x){
	if(a[x][0]>=l&&a[x][0]<=r)del(a[x][0]);
	swap(c[a[x][0]],a[x][1]);
	if(a[x][0]>=l&&a[x][0]<=r)ins(a[x][0]);
	return ;
}
int main(){
	register int n,m;
	n=read();m=read();
	base=pow(n,0.75)+1;
	for(register int i=1;i<=n;i++)c[i]=read();
	register int tot=0,tim=0;
	for(register int i=1;i<=m;i++){
		register char opt;
		register int x,y;
		cin>>opt;
		x=read();y=read();
		if(opt=='Q'){
			tot++;
			vis[i]=1;
			q[tot].id=i;
			q[tot].x=x;
			q[tot].y=y;
			q[tot].t=tim;
		}
		else{
			tim++;
			a[tim][0]=x;
			a[tim][1]=y;
		}
	}
	sort(q+1,q+tot+1);
	l=1;r=0;p=0;
	for(register int i=1;i<=tot;i++){
		int x=q[i].x,y=q[i].y,t=q[i].t;
		while(l<x)del(l++);
		while(l>x)ins(--l);
		while(r<y)ins(++r);
		while(r>y)del(r--);
		while(p<t)change(++p);
		while(p>t)change(p--);
		ANS[q[i].id]=ans;
	}
	for(register int i=1;i<=m;i++){
		if(!vis[i])continue;
		write(ANS[i]);
		if(!ANS[i])putchar('0');
		putchar('\n');
	}
	return 0;
}

树上莫队

COT2 - Count on a tree II

考虑一个神奇的序：欧拉序

就是dfs的时候不仅记录进栈的时间同时记录出栈的时间

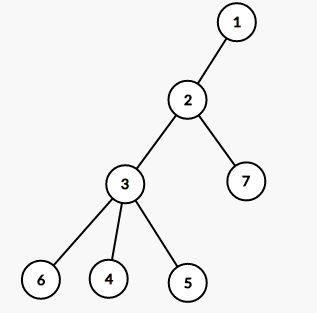
借用自为风月马前卒大佬blog的图

它跑出来的一个欧拉序是这样的

1 2 3 6 6 4 4 5 5 3 7 7 2 1

每个点第一次出现代表它在此时进栈，第二次出现代表它在此时出栈

我们可以定义st[i]表示i点的进栈时间，ed[i]表示i点的出栈时间

不妨设dep[x]<=dep[y]

考虑路径有两种情况

LCA(x,y)==x

此时我们需要的区间就是st[x]到st[y]或ed[y]到ed[x]的全部

同时该区间所有出现了两次的点都不要

我们思考出现两遍的点代表什么

出现两边证明我们遍历了该点的整棵子树并且x在其之前入栈，y在其之后入栈

那么这个点并不在x到y的路径中

而同时因为x是y的祖先，目前y还没退出去，那么y的所有祖先的出栈点应在更后面

而x之上的祖先在st[x]之前入栈，ed[x]之后出诊，故不影响我们的查询

LCA(x,y)!=x

我们需要的区间是ed[x]到st[y]，但由于这段区间不会包含LCA(x,y)，我们还要单独加上LCA(x,y)

我们思考从x退栈的过程，它会往祖先走然后去下一个子树

当遍历到y时，我们可以想象到

从x到lca(不包括lca)的点都出栈了，不在x到y路径的点都遍历了两遍，y到lca(不包括lca)的点都还没出栈

而st[lca]在st[x]之前，ed[lca]在ed[y]之后，lca不会出现在ed[x]到st[y]这个区间里

当我们确定了区间后跑普通莫队即可

而这个莫队是只记录出现奇数次的点的贡献的

无论是不出现还是出现两次都是不计算贡献

注意lca的特殊性

#include<bits/stdc++.h>
using namespace std;
const int maxn=40005,maxm=100005;
int block;
struct Query{
	int id;
	int x,y,z;
	bool operator <(Query i)const{
		return x/block==i.x/block?y<i.y:x<i.x;
	}
}q[maxm];
struct node{
	int id,data;
	bool operator <(node i)const{
		return data<i.data;
	}
}a[maxn];
struct Edge{
	int to;
	int nxt;
}e[2*maxn];
int cnt;
int head[maxn];
int c[maxn];
int dep[maxn],f[maxn][21];
int tp=0;
int s[2*maxn],st[maxn],ed[maxn];
int tot[maxn];
int ans=0;
int ANS[maxm];
bool vis[maxn];
int read(){
	int x=0,y=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
	while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	return x*y;
}
void add(int u,int v){
	e[cnt].to=v;
	e[cnt].nxt=head[u];
	head[u]=cnt++;
	return ;
}
void dfs(int x,int fa){
	s[++tp]=x;
	st[x]=tp;
	dep[x]=dep[fa]+1;
	f[x][0]=fa;
	for(int i=1;i<=20;i++)
		f[x][i]=f[f[x][i-1]][i-1];
	for(int i=head[x];i!=-1;i=e[i].nxt){
		int tmp=e[i].to;
		if(tmp==fa)continue;
		dfs(tmp,x);
	}
	s[++tp]=x;
	ed[x]=tp;
	return ;
}
int lca(int x,int y){
	if(dep[x]<dep[y])swap(x,y);
	for(int i=20;i>=0;i--)
		if(dep[f[x][i]]>=dep[y])
			x=f[x][i];
	if(x==y)return x;
	for(int i=20;i>=0;i--)
		if(f[x][i]!=f[y][i]){
			x=f[x][i];
			y=f[y][i];
		}
	return f[x][0];
}
void modify(int x){
	vis[s[x]]^=1;
	if(!vis[s[x]]){
		tot[c[s[x]]]--;
		if(tot[c[s[x]]]==0)ans--;
	}
	else{
		tot[c[s[x]]]++;
		if(tot[c[s[x]]]==1)ans++;
	}
	return ;
}
int main(){
	int n,m;
	n=read();m=read();
	block=sqrt(2*n);
	for(int i=1;i<=n;i++){
		a[i].id=i;
		a[i].data=read();
	}
	sort(a+1,a+n+1);
	int w=0;
	for(int i=1;i<=n;i++){
		if(a[i].data>a[i-1].data)w++;
		c[a[i].id]=w;
	}
	memset(head,-1,sizeof(head));
	for(int i=1;i<n;i++){
		int u,v;
		u=read();v=read();
		add(u,v);
		add(v,u);
	}
	dfs(1,0);
	for(int i=1;i<=m;i++){
		int u,v;
		u=read();v=read();
		int p=lca(u,v);
		q[i].id=i;q[i].z=0;
		if(p==u||p==v){
			if(st[v]<st[u])swap(u,v);
			q[i].x=st[u];q[i].y=st[v];
		}
		else{
			if(ed[v]<st[u])swap(u,v);
			q[i].x=ed[u];q[i].y=st[v];q[i].z=p;
		}
	}
	sort(q+1,q+m+1);
	int l=1,r=0;
	for(int i=1;i<=m;i++){
		int id=q[i].id,x=q[i].x,y=q[i].y,z=q[i].z;
		while(l<x)modify(l++);
		while(l>x)modify(--l);
		while(r<y)modify(++r);
		while(r>y)modify(r--);
		if(z)modify(st[z]);
		ANS[id]=ans;
		if(z)modify(st[z]);
	}
	for(int i=1;i<=m;i++)
		printf("%d\n",ANS[i]);
	return 0;
}

树上带修莫队

就树上莫队带个修改，写欧拉序后转变成序列带修莫队

[WC2013]糖果公园

#pragma GCC optimize(2)
#include<bits/stdc++.h>
using namespace std;
const int maxn=100005,maxm=100005;
int block;
struct Query{
	int id;
	int x,y,z,t;
	bool operator <(Query i)const{
		return ((x/block)^(i.x/block))?x<i.x:((y/block)^(i.y/block)?y<i.y:t<i.t);
	}
}q[maxm];
struct node{
	int id,data;
	bool operator <(node i)const{
		return data<i.data;
	}
}a[maxn];
struct Edge{
	int to;
	int nxt;
}e[maxn<<1];
int cnt;
int head[maxn];
long long val[maxn],w[maxn];
int c[maxn];
int upd[maxm][2];
int dep[maxn],f[maxn][18];
int tp=0;
int s[maxn<<1],st[maxn],ed[maxn];
int l,r;
int tot[maxn];
long long ans;
long long ANS[maxm];
bool vis[maxn];
inline int read(){
	register int x=0,y=1;
	register char ch=getchar();
	while(ch<'0'||ch>'9'){if(!(ch^'-'))y=-1;ch=getchar();}
	while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	return x*y;
}
inline void write(long long x){
	if(!x)return ;
	write(x/10);
	putchar(x%10+'0');
	return ;
}
inline void add(register int u,register int v){
	e[cnt].to=v;
	e[cnt].nxt=head[u];
	head[u]=cnt++;
	return ;
}
inline void dfs(register int x,register int fa){
	s[++tp]=x;
	st[x]=tp;
	dep[x]=dep[fa]+1;
	f[x][0]=fa;
	for(register int i=1;i<=17;i++){
		if(dep[x]<=(1<<i))break;
		f[x][i]=f[f[x][i-1]][i-1];
	}
	for(register int i=head[x];i!=-1;i=e[i].nxt){
		register int tmp=e[i].to;
		if(tmp==fa)continue;
		dfs(tmp,x);
	}
	s[++tp]=x;
	ed[x]=tp;
	return ;
}
inline int lca(register int x,register int y){
	if(dep[x]<dep[y])swap(x,y);
	for(register int i=17;i>=0;i--)
		if(dep[f[x][i]]>=dep[y])
			x=f[x][i];
	if(x==y)return x;
	for(register int i=17;i>=0;i--)
		if(f[x][i]^f[y][i]){
			x=f[x][i];
			y=f[y][i];
		}
	return f[x][0];
}
inline void modify(register int x){
	vis[s[x]]^=1;
	if(!vis[s[x]]){
		ans-=w[tot[c[s[x]]]]*val[c[s[x]]];
		tot[c[s[x]]]--;
		ans+=w[tot[c[s[x]]]]*val[c[s[x]]];
	}
	else{
		ans-=w[tot[c[s[x]]]]*val[c[s[x]]];
		tot[c[s[x]]]++;
		ans+=w[tot[c[s[x]]]]*val[c[s[x]]];
	}
	return ;
}
inline void update(register int x){
	register int tmp1=st[upd[x][0]],tmp2=ed[upd[x][0]];
	if(tmp1>=l&&tmp1<=r)modify(tmp1);
	if(tmp2>=l&&tmp2<=r)modify(tmp2);
	swap(c[s[tmp1]],upd[x][1]);
	if(tmp1>=l&&tmp1<=r)modify(tmp1);
	if(tmp2>=l&&tmp2<=r)modify(tmp2);
	return ;
}
int main(){
	register int n,co,m;
	n=read();co=read();m=read();
	for(int i=1;i<=co;i++)val[i]=read();
	for(int i=1;i<=n;i++)w[i]=w[i-1]+read();
	for(int i=1;i<=n;i++)head[i]=-1;
	for(register int i=1;i<n;i++){
		register int u,v;
		u=read();v=read();
		add(u,v);
		add(v,u);
	}
	for(register int i=1;i<=n;i++)c[i]=read();
	dfs(1,0);
	register int tim=0,que=0;
	for(register int i=1;i<=m;i++){
		register int type,u,v;
		type=read();u=read();v=read();
		if(type){
			que++;
			register int p=lca(u,v);
			q[que].id=que;q[que].z=0;q[que].t=tim;
			if(p==u||p==v){
				if(st[v]<st[u])swap(u,v);
				q[que].x=st[u];q[que].y=st[v];
			}
			else{
				if(ed[v]<st[u])swap(u,v);
				q[que].x=ed[u];q[que].y=st[v];q[que].z=p;
			}
		}
		else{
			tim++;
			upd[tim][0]=u;
			upd[tim][1]=v;
		}
	}
	block=pow(n,tim?2.0/3:1.0/2);
	sort(q+1,q+que+1);
	register int p=0;
	l=1;r=0;
	for(register int i=1;i<=que;i++){
		register int id=q[i].id,x=q[i].x,y=q[i].y,z=q[i].z,t=q[i].t;
		while(l<x)modify(l++);
		while(l>x)modify(--l);
		while(r<y)modify(++r);
		while(r>y)modify(r--);
		while(p<t)update(++p);
		while(p>t)update(p--);
		if(z)modify(st[z]);
		ANS[id]=ans;
		if(z)modify(st[z]);
	}
	for(register int i=1;i<=que;i++){
		write(ANS[i]);
		if(!ANS[i])putchar('0');
		putchar('\n');
	}
	return 0;
}

回滚莫队

我们可能遇到一些毒瘤题

发现增加或者删除很简单，而另一操作几乎不可做

回滚莫队应运而生

最经典的就是求max/min

对于加入显然容易，但删除就不好维护了

【模板】回滚莫队&不删除莫队

我们考虑维护三个东西，每个数字出现个数，每个数字在此区间最早出现位置和最晚出现位置

我们要保证我们的区间基本都在扩大

单独处理左右边界在同块的情况，sqrt(n)可以解决

考虑当左指针在同块时，右指针递增

我们每一次操作都让左指针从该块的右端点出发往左走，这样对于所有在同块的情况就能只用增加区间了

而对于左指针换块时

我们令左右指针都到该块的右边界去

由于同块的左右边界被我们单独处理掉了

我们剩下的询问一定只用增加区间了

每次左指针回块右边界时记得清理信息

#include<bits/stdc++.h>
using namespace std;
const int maxn=200005,maxm=200005;
int block;
struct node{
	int id,data;
	bool operator <(node i)const{
		return data<i.data;
	}
}a[maxn];
struct Query{
	int id;
	int x,y;
	bool operator <(Query i)const{
		return ((x-1)/block+1)^((i.x-1)/block+1)?x<i.x:y<i.y;
	}
}q[maxm];
int c[maxn];
int cur[maxn][3],tmp[maxn][3],k[maxn][2];
int ANS[maxm];
int read(){
	int x=0,y=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
	while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	return x*y;
}
int get(int x){
	return (x-1)/block+1;
}
void ins(int t[maxn][3],int x,int &ans){
	t[c[x]][0]++;
	if(t[c[x]][0]>=1){
		t[c[x]][1]=min(t[c[x]][1],x);
		t[c[x]][2]=max(t[c[x]][2],x);
		ans=max(ans,t[c[x]][2]-t[c[x]][1]);
	}
	return ;
}
void del(int t[maxn][3],int x){
	t[c[x]][0]--;
	return ;
}
int main(){
	int n,m;
	n=read();
	block=sqrt(n);
	for(int i=1;i<=n;i++){a[i].id=i;a[i].data=read();}
	sort(a+1,a+n+1);
	int w=0;
	a[0].data=0;
	for(int i=1;i<=n;i++){
		if(a[i].data>a[i-1].data)w++;
		c[a[i].id]=w;
	}
	m=read();
	for(int i=1;i<=m;i++){
		q[i].id=i;
		q[i].x=read();q[i].y=read();
	}
	sort(q+1,q+m+1);
	int l=1,r=0,last=0,ans=0;
	for(int i=1;i<=w;i++)cur[i][1]=tmp[i][1]=n+1;
	for(int i=1;i<=m;i++){
		int id=q[i].id,x=q[i].x,y=q[i].y,d=0;
		if(get(x)==get(y)){
			for(int j=x;j<=y;j++)ins(tmp,j,d);
			for(int j=x;j<=y;j++)del(tmp,j);
			for(int j=x;j<=y;j++){tmp[c[j]][1]=n+1;tmp[c[j]][2]=0;}
			ANS[id]=d;
			continue;
		}
		if(get(x)^last){
			for(int j=1;j<=w;j++){
				cur[j][0]=0;
				cur[j][1]=n+1;
				cur[j][2]=0;
			}
			l=get(x)*block;
			r=get(x)*block-1;
			ans=0;
			last=get(x);
		}
		while(r<y)ins(cur,++r,ans);
		d=ans;
		int pos=l;
		for(int j=x;j<l;j++){
			k[c[j]][0]=cur[c[j]][1];
			k[c[j]][1]=cur[c[j]][2];
		}
		while(pos>x)ins(cur,--pos,d);
		while(pos<l)del(cur,pos++);
		for(int j=x;j<l;j++){
			cur[c[j]][1]=k[c[j]][0];
			cur[c[j]][2]=k[c[j]][1];
		}
		ANS[id]=d;
	}
	for(int i=1;i<=m;i++)printf("%d\n",ANS[i]);
	return 0;
}

Rmq Problem / mex

求mex也时莫队的经典用法

我们发现删除一个值很容易

考虑搞一个不增加莫队

左指针每次在块的左边界，右指针对于一个块从n开始往左跑

排序时保证右端点递减

类比不删除莫队

#include<bits/stdc++.h>
using namespace std;
const int maxn=200005,maxm=200005;
int block;
struct Query{
	int id;
	int x,y;
	bool operator <(Query i)const{
		return ((x-1)/block+1)^((i.x-1)/block+1)?x<i.x:y>i.y;
	}
}q[maxm];
struct node{
	int id,data;
	bool operator <(node i)const{
		return data<i.data;
	}
}a[maxn];
int c[maxn],val[maxn];
int ANS[maxm];
int cnt[maxn],tot[maxn];
inline int read(){
	register int x=0,y=1;
	register char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
	while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	return x*y;
}
inline int get(register int x){
	return (x-1)/block+1;
}
inline void del(register int *t,register int x,register int &ans){
	t[c[x]]--;
	if(t[c[x]]==0)ans=min(ans,val[c[x]]);
	return ;
}
inline void ins(register int *t,register int x){
	t[c[x]]++;
	return ;
}
int main(){
	register int n,m;
	n=read();m=read();
	block=sqrt(n);
	for(register int i=1;i<=n;i++){a[i].id=i;a[i].data=read();}
	sort(a+1,a+n+1);
	int w=0;
	a[0].data=-1;
	val[0]=-1;
	for(register int i=1;i<=n;i++){
		if(a[i].data>a[i-1].data)w++;
		c[a[i].id]=w;
		val[w]=a[i].data;
	}
	for(register int i=1;i<=m;i++){
		q[i].id=i;
		q[i].x=read();q[i].y=read();
	}
	sort(q+1,q+m+1);
	register int l=1,r=0,last=0,ans=0;
	for(int i=1;i<=m;i++){
		register int id=q[i].id,x=q[i].x,y=q[i].y,tmp=0;
		if(get(x)^last){
			while(l<max((get(x)-1)*block,1))del(cnt,l++,ans);
			while(r<n)ins(cnt,++r);
			ans=-1;
			for(register int j=1;j<=w;j++){
				if(val[j]-val[j-1]>1){ans=val[j-1]+1;break;}
				if(cnt[j]==0){ans=val[j];break;}
			}
			if(ans==-1)ans=val[w]+1;
			last=get(x);
		}
		if(get(x)==get(y)){
			for(register int j=x;j<=y;j++)ins(tot,j);
			tmp=-1;
			for(register int j=1;j<=w;j++){
				if(val[j]-val[j-1]>1){tmp=val[j-1]+1;break;}
				if(tot[j]==0){tmp=val[j];break;}
			}
			if(tmp==-1)tmp=val[w]+1;
			ANS[id]=tmp;
			for(register int j=x;j<=y;j++)del(tot,j,tmp);
			continue;
		}
		while(r>y)del(cnt,r--,ans);
		tmp=ans;
		register int pos=l;
		while(pos<x)del(cnt,pos++,tmp);
		while(pos>l)ins(cnt,--pos);
		ANS[id]=tmp;
	}
	for(register int i=1;i<=m;i++)
		printf("%lld\n",ANS[i]);
	return 0;
}

[MdOI2020] Path

回滚莫队+01trie

solution

#include<bits/stdc++.h>
using namespace std;
const int maxn=30005;
int block;
struct Query{
	int id,x,y;
	bool operator <(Query i)const{
		return ((x-1)/block==(i.x-1)/block)?y<i.y:x<i.x;
	}
}q[2*maxn];
struct Edge{
	int to,w;
	int nxt;
}e[2*maxn];
int cnt;
int head[maxn];
int a[maxn];
int dfsnum=0;
int c[2*maxn];
int dfn[maxn],son[maxn];
int cur=0;
int tot1,tot2;
int trie1[32*maxn][3],trie2[32*maxn][3];
int ANS[maxn];
int read(){
	int x=0,y=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
	while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	return x*y;
}
void add(int u,int v,int w){
	e[cnt].to=v;
	e[cnt].w=w;
	e[cnt].nxt=head[u];
	head[u]=cnt++;
	return ;
}
void dfs(int x,int fa){
	c[++dfsnum]=x;
	dfn[x]=dfsnum;
	son[x]=1;
	for(int i=head[x];i!=-1;i=e[i].nxt){
		int tmp=e[i].to;
		if(tmp==fa)continue;
		a[tmp]=(a[x]^e[i].w);
		dfs(tmp,x);
		son[x]+=son[tmp];
	}
	return ;
}
int get(int x){
	return (x-1)/block+1;
}
int query(int trie[32*maxn][3],int x){
	int k=0,ans=0;
	for(int i=30;i>=0;i--){
		int to=(((x>>i)&1)^1);
		if(!trie[k][to])to^=1;
		else ans+=(1<<i);
		k=trie[k][to];
	}
	return ans;
}
void ins(int trie[32*maxn][3],int &tot,int x,int &ans){
	ans=max(ans,query(trie,x));
	int k=0;
	trie[k][2]++;
	for(int i=30;i>=0;i--){
		int to=((x>>i)&1);
		if(!trie[k][to])trie[k][to]=++tot;
		k=trie[k][to];
		trie[k][2]++;
	}
	return ;
}
void del(int trie[32*maxn][3],int x){
	int k=0;
	trie[k][2]--;
	for(int i=30;i>=0;i--){
		int to=((x>>i)&1);
		int fa=k;
		k=trie[k][to];
		trie[k][2]--;
		if(!trie[k][2])trie[fa][to]=0;
	}
	return ;
}
int main(){
	int n;
	n=read();
	block=sqrt(n);
	memset(head,-1,sizeof(head));
	for(int i=1;i<n;i++){
		int u,v,w;
		u=read();v=read();w=read();
		add(u,v,w);
		add(v,u,w);
	}
	dfs(1,0);
	for(int i=n+1;i<=2*n;i++)c[i]=c[i-n];
	for(int i=1;i<n;i++){
		q[i].id=i+1;q[i].x=dfn[i+1];q[i].y=dfn[i+1]+son[i+1]-1;
		q[i+n-1].id=i+1;q[i+n-1].x=dfn[i+1]+son[i+1];q[i+n-1].y=n+dfn[i+1]-1;
	}
	sort(q+1,q+2*(n-1)+1);
	int l=1,r=0,last=0;
	for(int i=1;i<2*n-1;i++){
		int id=q[i].id,x=q[i].x,y=q[i].y,tmp=0;
		if(get(x)==get(y)){
			for(int j=x;j<=y;j++)ins(trie2,tot2,a[c[j]],tmp);
			for(int j=x;j<=y;j++)del(trie2,a[c[j]]);
			tot2=0;
			ANS[id]+=tmp;
			continue;
		}
		if(last<get(x)){
			l=get(x)*block;
			r=get(x)*block-1;
			for(int j=0;j<=tot1;j++)trie1[j][0]=trie1[j][1]=trie1[j][2]=0;
			tot1=0;
			cur=0;
			last=get(x);
		}
		while(r<y)ins(trie1,tot1,a[c[++r]],cur);
		int p=l;
		tmp=cur;
		while(p>x)ins(trie1,tot1,a[c[--p]],tmp);
		while(p<l)del(trie1,a[c[p++]]);
		ANS[id]+=tmp;
	}
	int sum=0;
	for(int i=2;i<=n;i++)
		sum=max(sum,ANS[i]);
	printf("%d\n",sum);
	return 0;
}

二次离线莫队

lxl大佬提出的用于解决莫队转移复杂度较高问题的神奇操作

【模板】莫队二次离线（第十四分块(前体)）

例如此题

我们很容易得出n根号带个组合数的复杂度

这是爆炸的

设一次转移复杂度为k

我们考虑莫队转移时有4种情况

[l,r]变成[l,r+1]时的情况分析如下

记f(x,[l,r])表示a[x]与[l,r]所构成的答案

进行容斥

$\Delta ans=f(r+1,[l,r])=f(r+1,[1,r])-f(r+1,[1,l-1])\\ \Delta ans是答案的变化量，这里参考普通莫队的实现$

我们发现f(i,[1,i-1])可以对于每一个i预处理出来

预处理的复杂度O(nk)

而对于减去的f我们考虑把r+1这个点挂在l-1上

而对于普遍的莫队转移应是[l,r]变为[l,r+p]

那么任意i属于[r+1,r+p]都应挂在l-1上去求f(i,[1,l-1])这个值

我们用一个vector来解决挂这个事情

接下来从1到n去枚举挂了区间的点i

由于普通莫队复杂度为n带个根号

也就是说左右指针移动次数是n带个根号级别

那么我们去扫每一个挂在某一个点上的区间最终的复杂度将也是n带个根号

对于把[1,i]这个区间处理好是O(k)的(我们已处理好[1,i-1])

故此操作复杂度O(nk)

而去扫每一个区间总复杂度是O(nsqrt(n))的

故总复杂度O(nsqrt(n)+nk)

我们刚刚只考虑了从[l,r]变到[l,r+p]这样转移的情况

初学的我见到大佬的blog基本都只讨论了此一种情况让天真的我以为只有这一种情况

我就是菜

我们可以尝试再讨论一种因为我懒得讨论完

从[l,r]变为[l+p,r]

考虑任意i属于[l+1,l+p]

$\Delta ans=f(i,[i+1,r])=f(i,[1,r])-f(i,[1,i])$

我们发现f(i,[1,i])可以预处理搞定

我们可以把[l+1,l+p]这个区间挂到r上进行一样操作就行了

接下来还有两种情况基本相同

不同的题的分类和需要预处理的东西可能有所不同

但核心思想就是通过容斥把答案分成两部分算

一部分直接预处理得到

另一部分通过二次离线的处理得到

使原本的O(nsqrt(n)k)降至O(nsqrt(n)+nk)

这里放一下代码

一些需要注意的地方在代码里均有标注

#pragma GCC diagnostic error "-std=c++14"
#pragma GCC target("avx")
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#include<bits/stdc++.h>
using namespace std;
const int maxn=100005,maxm=100005;
int block;
struct Query{
	int id,x,y;
	bool operator <(Query i)const{
		return ((x-1)/block==(i.x-1)/block)?y<i.y:x<i.x;
	}
}q[maxm];
struct seq{
	int l,r,id,op;
};
short a[maxn];
int tot;
int c[1<<14];
int t[1<<14];//t[i]的定义为值为i在当前区间中的答案
long long pre1[maxn],pre2[maxn];
long long ans[maxm],out[maxm];
vector<seq>v[maxn];
inline int read(){
	register int x=0,y=1;
	register char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
	while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	return x*y;
}
inline void write(register long long x){
	if(!x)return ;
	write(x/10);
	putchar(x%10+'0');
	return ;
}
inline int lowbit(register int x){
	return x&-x;
}
inline int one(register int x){
	register int ans=0;
	while(x){
		x-=lowbit(x);
		ans++;
	}
	return ans;
}
int main(){
	register int n,m,k;
	register short maxa=0;
	n=read();m=read();k=read();
	if(k>14){
		for(register int i=1;i<=m;i++){putchar('0');putchar('\n');}
		return 0;
	}
	block=sqrt(n);
	for(register int i=1;i<=n;i++){
		a[i]=read();
		maxa=max(maxa,a[i]);
	}
	for(int i=13;i>=0;i--)
		if((1<<i)<=maxa){maxa=i;break;}
	for(register int i=0;i<(1<<maxa+1);i++)
		if(one(i)==k)c[++tot]=i;
	for(register int i=1;i<=n;i++){
		pre1[i]=pre1[i-1]+t[a[i]];
		for(register int j=1;j<=tot;j++)t[a[i]^c[j]]++;
		pre2[i]=pre2[i-1]+t[a[i]];//注意上面讨论的有f(i,[1,i])即i也要算进去
	}
	for(register int i=1;i<=m;i++){
		q[i].id=i;
		q[i].x=read();q[i].y=read();
	}
	sort(q+1,q+m+1);
	q[0].x=1;q[0].y=0;
	for(register int i=1;i<=m;i++){
		register int l=q[i-1].x,r=q[i-1].y;
		register int x=q[i].x,y=q[i].y;
		ans[i]=pre1[y]-pre1[r]+pre2[x-1]-pre2[l-1];
		if(y<r)
			v[l-1].push_back((seq){y+1,r,i,1});
		else if(y>r)
			v[l-1].push_back((seq){r+1,y,i,-1});
		if(x<l)
			v[y].push_back((seq){x,l-1,i,1});
		else if(x>l)
			v[y].push_back((seq){l,x-1,i,-1});
        //这里是默认先把r移到了y在去移动l，故挂在y点上
	}
	memset(t,0,sizeof(t));
	for(register int i=1;i<=n;i++){
		for(register int j=1;j<=tot;j++)t[a[i]^c[j]]++;
		for(register int j=0;j<v[i].size();j++){
			seq o=v[i][j];
			register int l=o.l,r=o.r,id=o.id,op=o.op;
			register long long tmp=0;
			for(register int p=l;p<=r;p++)tmp+=t[a[p]];
			ans[id]+=op*tmp;
		}
	}
	for(register int i=1;i<=m;i++){ans[i]+=ans[i-1];out[q[i].id]=ans[i];}
    //我们在上面考虑的都是ans的变化量，故应该再求前缀和
	for(register int i=1;i<=m;i++){
		if(!out[i])putchar('0');
		else write(out[i]);
		putchar('\n');
	}
	return 0;
}