竞赛图学习笔记

大概只写了一点点性质，也许会更多了会来更

定义

竞赛图即有向完全图

性质

1. 竞赛图缩点后DAG图呈链状，每个点向其后所有点连边

   这比较显然

2. 竞赛图中存在一条哈密顿路径

   考虑归纳，对于 n=1,2,3命题成立

   若结论在 $n=k-1$ 时成立，考虑加入点 $k$

   若新点连向原路径起点，则存在新路径，若原路径终点连向新点，同理

   否则，按顺序考虑新点与原路径点的连边，由于 $d_1\to k,k\to d_{k-1}$ 故存在 $d_i\to k,k\to d_{i+1}$

   则原命题成立

3. 竞赛图存在一条哈密顿回路当且仅当其强连通

   若其存在哈密顿回路显然强连通

   考虑证明强连通竞赛图一定有哈密顿回路并给出一种构造方法

   考虑找到一条哈密顿路径 $s\to t$

   由于竞赛图强连通，找到路径上第一个条 $x\to s$ 的边，显然存在这样的 $x$

   考虑扩展到 $nxt_x$

   • 若存在 $(nxt_x,s)$ ，回路扩展

   • 若存在 $(nxt_x,i),i\in Circle$ ，回路亦可扩展

     

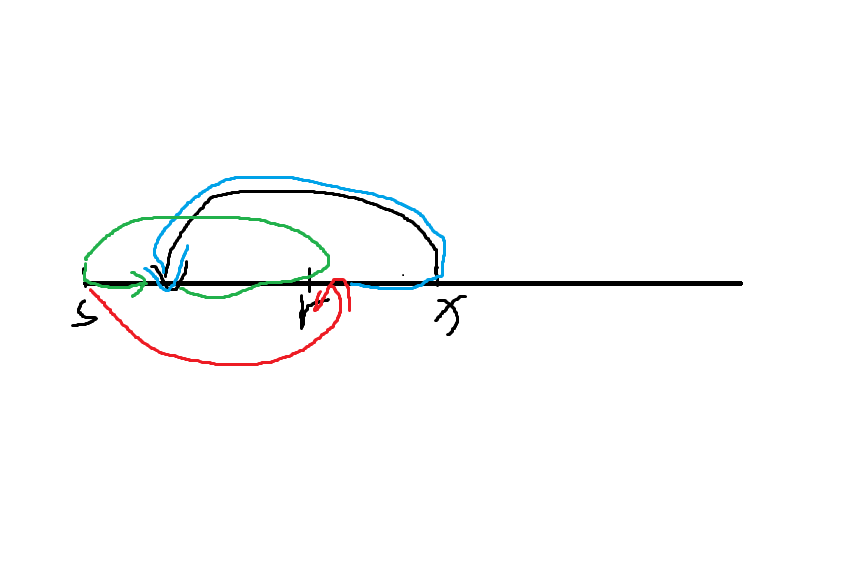
     ​ 上图回路扩展为红，蓝，绿（$s\to r$ 的哈密顿回路）

   • 否则，不做操作，之后一定存在点 $y$ 满足前两种情况

   $t$ 点一定属于Case1,2

   故得到了一个哈密顿回路

4. 大小为 $n$ 的强连通竞赛图存在大小为 $[3,n]$ 的环

   运用归纳，通过性质3可证

5. 判断竞赛图强连通的高效方法

   将顶点出度序列升序排列，竞赛图强连通等价于不存在 $k<n$ 满足前 $k$ 个出度之和等于 $\tbinom k 2$

   判断时间复杂度 $O(nlogn)$，朴素tarjan $O(n^2)$

   考虑若竞赛图非强连通，则存在不止一个scc，由性质1

   出度序列升序排列后，链后点一定在链前点之前，我们只需判断最后一个scc大小即可

   容易发现该做法的正确性