后缀系列

后缀数组SA

问题

$sa_i$定义为字符串所有后缀按字典序排序后排名为$i$的串的起始位置，求出$sa_i$

求解

后缀数组有两种求法，一种是常用的倍增法，另一种是常数贼大的线性做法$\text{DC3}$
由于倍增法好写好调，一般使用倍增法求后缀数组

我们考虑枚举长度$k$，假如我们已经得到了$S[i,i+k-1]$串的$sa$数组
那么我们的问题实际上变成了一个双关键字排序的问题
第一关键字为$sa_i$，第二关键字为$sa_{i+k}$
记第一关键字为$x_i$，第二关键字为$y_i$
这里可以用$\text{sort}$，时间复杂度$O(nlog^2n)$
但我们可以用到更优秀的基数排序，$O(n)$的实现排序
不了解基数排序可以简单理解为桶排

for(int i=1;i<=n;i++)t[x[i]=s[i]]++;
for(int i=1;i<=m;i++)t[i]+=t[i-1];
for(int i=n;i>=1;i--)sa[t[x[i]]--]=i;//倒序把数塞入它的排名，不难理解

由于我们需要先按第一关键字排，再按第二关键字排
而基数排序是稳定的排序，及若$a_i==a_j,i<j$，排序后仍满足$i<j$
我们利用这一点，先排第二关键字，再排第一关键字
由于基数排序的稳定性若$x_i==x_j$，$y_i<y_j$则$i<j$

部分代码

//y[i]是第二关键字排名为i的第一关键字起始位置
int len=0;
for(int i=n-k+1;i<=n;i++)y[++len]=i;//无第二关键字，排在最前面
for(int i=1;i<=n;i++)if(sa[i]>k)y[++len]=sa[i]-k;//有第二关键字，按第二关键字排序
for(int i=1;i<=m;i++)t[i]=0;
for(int i=1;i<=n;i++)t[x[y[i]]]++;//放入桶中
for(int i=1;i<=m;i++)t[i]+=t[i-1];//求前缀和
for(int i=n;i>=1;i--)sa[t[x[y[i]]]--]=y[i],y[i]=0;//得到sa数组

至此，我们还需要得到下一个$k$的$x$数组即可

完整代码

for(int i=1;i<=n;i++)t[x[i]=s[i]]++;
for(int i=1;i<=m;i++)t[i]+=t[i-1];
for(int i=n;i>=1;i--)sa[t[x[i]]--]=i;
for(int k=1;k<=n;k<<=1){
    int len=0;
    for(int i=n-k+1;i<=n;i++)y[++len]=i;
    for(int i=1;i<=n;i++)if(sa[i]>k)y[++len]=sa[i]-k;
    for(int i=1;i<=m;i++)t[i]=0;
    for(int i=1;i<=n;i++)t[x[y[i]]]++;
    for(int i=1;i<=m;i++)t[i]+=t[i-1];
    for(int i=n;i>=1;i--)sa[t[x[y[i]]]--]=y[i],y[i]=0;
    swap(x,y);
    len=0;
    x[sa[1]]=++len;
    for(int i=2;i<=n;i++)
        x[sa[i]]=(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])?len:++len;
    if(len==n)break;
    m=len;
}

应用

$\text{LCP}$

最长公共前缀
定义$\text{LCP(i,j)}$表示后缀排序后第$i$个串与第$j$个串的最长公共前缀
这东西我们不好求
考虑这是一个排序后的字符串
不难发现$\text{LCP(i,j)}=\min_{k=i+1}^{j} \text{LCP(k-1,k)}$

这个式子的证明等价于证明$\text{LCP(i,j)}=\min \text{LCP(i,k)},\text{LCP(k,j)}$

记$x=\min \text{LCP(i,k)},\text{LCP(k,j)}$
$i$串与$k$串最长公共前缀大于等于$x$，$k$串与$j$串最长公共前缀大于等于$x$
故$\text{LCP(i,j)}>=x$
若$\text{LCP(i,j)}>x$，则$x>x$矛盾

定义$height_i$=$\text{LCP(i-1,i)}$
问题转化为求$height$数组后$\text{st}$表$\text{O(1)}$求解

考虑到排序后的字串之间没有前后缀性质
定义辅助数组$h_i=height_{rk_i},sa_{rk_i}=i$
$h_i$为$i$开头的后缀串排序后的位置和该位置前一个的最长公共前缀

得到单调性后$O(n)$扫一边即可

void get_height(){
	for(register int i=1;i<=n;i++)rk[sa[i]]=i;
	register int k=0;
	for(register int i=1;i<=n;i++){
		if(rk[i]==1)continue;
		if(k)k--;
		register int j=sa[rk[i]-1];
		while(j+k<=n&&i+k<=n&&s[i+k]==s[j+k])k++;
		height[rk[i]]=k;
	}
	lg[0]=-1;
	for(register int i=1;i<=n;i++)st[0][i]=height[i],lg[i]=lg[i>>1]+1;
	for(register int j=1;j<=17;j++)
		for(register int i=1;i<=n-(1<<j)+1;i++)
			st[j][i]=min(st[j-1][i],st[j-1][i+(1<<j-1)]);
	return ;
}

后缀自动机SAM

定义

一个字符串S的SAM是一个接受所有S后缀的最小DFA（确定性有限自动机或确定性有限状态自动机）。
简单的认为一个SAM由两部分组成，即一个DAWG（有向单词无环图）和一颗parent树

DAWG中每个节点表示若干个S的子串特别的，起点代表空串
DAWG中的边称为转移边，每条转移边上有且仅有一个字符
x点的c转移边表示为 $to_{x,c}$
从起点出发，每条路径都会唯一对应一个S的子串
一个节点代表的字符串集合是S串的某个前缀的连续长度的若干后缀串集合
记节点 $x$ 所代表的最长字符串长度为 $max_x$，最短字符串长度为 $min_x$，其代表的所有串在S中末尾出现的位置集合应相同，称这个末尾集合为 $endpos_x$
任意两节点的endpos集合应互不相同

定义节点 $u$ 的parent指针指向 $v$，
当且仅当 $min_u=max_v+1$，且 $v$ 节点代表的子串均为 $u$节点代表子串的后缀，记作$nxt_u=v$
显然这是一个树形结构
显然在这颗parent树中子节点的endpos集合一定是父节点的endpos集合的真子集

构建

SAM的构建一般采用增量法
即通过S串的SAM构建出S+c串的SAM
特别的，另空串的SAM为单独的一个节点，标号为1
1号点也是SAM的起点
考虑到仅增加了|S|个后缀串
若表示S串的节点为 $p$ 节点，增加c字符后，只会影响p到parent根的一条路径

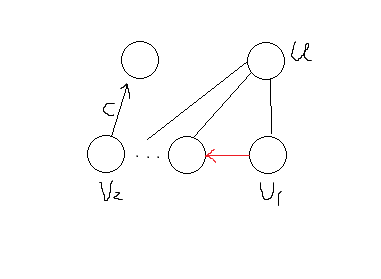
令 $p=v_1$，$v_2$ 为p到parent根路径上的第一个有字符c出边的点，$d$ 为 $to_{v_2,c}$
此时，我们只需将路径上 $v_2$ 前的点一直到 $v_1$ 都向新点 $u$ 连一条字符c的转移边即可
$u$ 代表的字符集即 $v_2$ 前的点一直到 $v_1$所代表字符集后边均加一个字符c
由于这些点之前没有c转移边，故 $u$ 的endpos只是|S|+1一个位置
$max_u=max_p+1,min_u=max_{v2}+2$

接下来考虑 $u$ 点的parent树上父亲

1. 不存在 $v_2$ 点
   $nxt_{v_2}=1$
   显然，因为此时 $u$ 点代表了|S|+c串的所有后缀串
2. 存在 $v_2$ 点，且满足 $max_d=max_{v_2}+1$
   此时，d点表示的所有串应该都为u的后缀且$min_u=max_d+1$
   则$nxt_u=d$
3. 存在 $v_2$ 点，且不满足 $max_d=max_{v_2}+1$
   那么 $max_d$ 一定大于 $max_{v_2}+1$
   由于这时d点所表示的最大串的某一段连续后缀的结束位置集合多了|S|+1这个位置
   不能单单用一个d点来承载这些信息了
   拆除一个点v来，$max_v=max_{v_2}+1,min_v=min_d$
   原d点变为 $min_d=max_v+1,max_d=max_d$
   此时$nxt_v=nxt_d,nxt_d=v,nxt_u=v$
   接下来由于d点所代表的串有变
   在p到根的路径里比 $v_2$ 深度更浅的点中能一步转移至d点的，都应该改成转移至v点

SAM的复杂度笔者并不会算，大概有机会了再补
其时间复杂度 $O(|S||\Sigma|)$，$|\Sigma|$ 为字符集大小

int to[maxn<<1][26],len[maxn<<1];
//实际实现只需要max即可，因为min[x]就是max[nxt[x]]，这里的len[x]即max[x]
int nxt[maxn<<1];
int tot=1;
int last=1;
void extend(int c){
	int p=last,u=++tot;
	len[u]=len[p]+1;
	while(p&&to[p][c]==0){to[p][c]=u;p=nxt[p];}//找到v2
	if(!p)nxt[u]=1;//Case1，不存在v2
	else{
		int d=to[p][c];
		if(len[d]==len[p]+1)nxt[u]=d;//Case2
		else{//Case3
			int v=++tot;
			for(int i=0;i<26;i++)to[v][i]=to[d][i];
			len[v]=len[p]+1;
			nxt[v]=nxt[d];nxt[d]=v;nxt[u]=v;
			while(p&&to[p][c]==d){to[p][c]=v;p=nxt[p];}
		}
	}
	last=u;
	return ;
}