从入门到进阶
二分图的定义
即没有奇环的图
可以分成两边,同侧的点无边相连,异侧的点可以有边

二分图的判定
根据定义,没有奇环的图即二分图
我们可以跑一边dfs给每个点染色
当我们接下来要去的点颜色和当前点相同即有奇环
bool dfs(int x,int co){
c[x]=co;
for(int i=head[x];i!=-1;i=e[i].nxt){
int tmp=e[i].to;
if(c[tmp]==(co^1))continue;
if(c[tmp]==co||dfs(tmp,co^1))return 1;
}
return 0;
}
二分图的最大匹配
这是二分图最基础以及重要的东西了
匹配:
最大匹配:
所有匹配中边数最大的匹配即最大匹配
说人话:
对于一个二分图,我们选出最多的边,使得边与边无公共点
这个问题我们可以用匈牙利算法解决
最坏情况下O(mn),m为边数,n为点数
这个算法的核心思想在于增广路
我们对于左边的每一个点去dfs
看它是否能跟右边未匹配的点匹配上
当它发现右边的某点点已经被匹配过后
它会去看看那个对方所匹配的点能否换一个人匹配
然后一直递归下去
如果最后的点和另外的点匹配成功了
那么这条路径上的点都能换一个点匹配成功
最后我们的第一个点就能匹配上了,即最大匹配数增加了
这样的一条路径被称为增广路
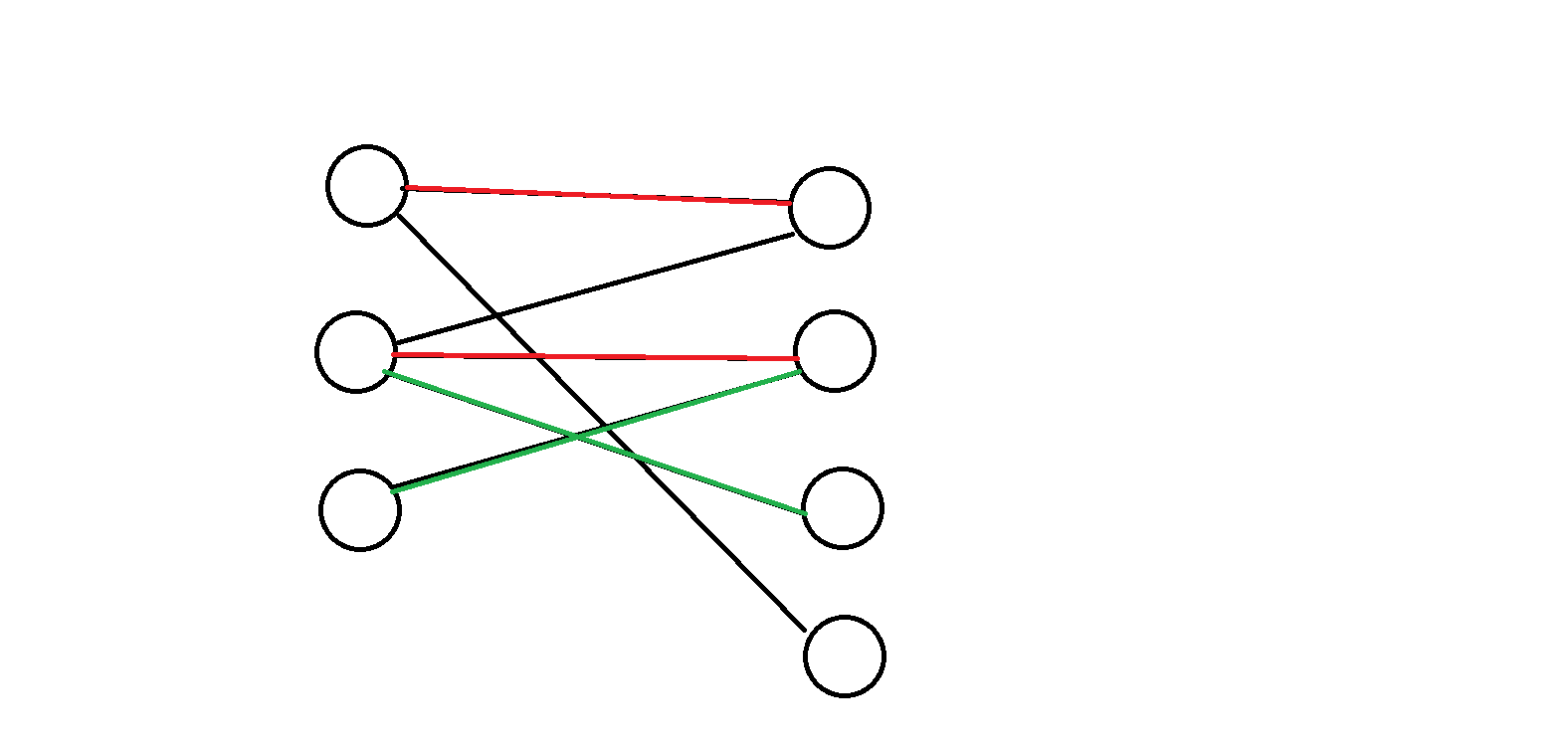
上图红边为原本的匹配
绿边为我们跑了一次增广路径后的匹配
我们把左边第二个点的匹配边更换了
具体实现如下
#include<bits/stdc++.h>
using namespace std;
const int maxn=1005,maxm=1005,maxedge=1000005;
struct Edge{
int to;
int nxt;
}e[2*maxedge];
int cnt;
int head[maxn+maxm];
int p[maxn+maxm];
bool vis[maxn+maxm];
int read(){
int x=0,y=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
return x*y;
}
void add(int u,int v){
e[cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt++;
return ;
}
bool dfs(int x){
for(int i=head[x];i!=-1;i=e[i].nxt){
int tmp=e[i].to;
if(vis[tmp])continue;
vis[tmp]=1;
if((!p[tmp])||dfs(p[tmp])){
p[tmp]=x;
return 1;
}
}
return 0;
}
int main(){
int n,m,edge;
n=read();m=read();edge=read();
memset(head,-1,sizeof(head));
for(int i=1;i<=edge;i++){
int u,v;
u=read();v=read();
if(u>n||v>m)continue;
add(u,v+n);
}
int ans=0;
for(int i=1;i<=n;i++){
memset(vis,0,sizeof(vis));
ans+=dfs(i);
}
printf("%d",ans);
return 0;
}
二分图的最大匹配还有一个重要求法
网络瘤流
就是建立一个源点向所有左边的点连容量为1的边
所有右边的点向汇点连容量为1的边
中间的边都容量为1
跑出来的最大流就是最大匹配
二分图的多重匹配
我们在上述的二分图匹配中每个点最多被匹配一次
若每个点能被匹配多次这样的问题称为二分图多重匹配问题
二分图的多重最大匹配用网络流解决
在建边时源点连出给左边点的边容量应是该点最多能被匹配的次数,汇点同理
二分图的其他重要定义
坐稳了
二分图最小点覆盖数
使得每一条边都至少有一个点被选的最小点数
二分图最大点独立集数
使得每一条边都至多有一个点被选的最大点数
最大团数
在一个无向图中,使得选中的点集两两有边的最大点数
求法:对于一个无向图学术界暂时没有多项式求法(似乎是这样),但若补图为二分图能求
补图即对于任意两点若原图有边,补图无边,原图无边,补图有边
求补图的最大点独立集即为最大团答案
结论:
最小点覆盖数=最大匹配数
最大点独立集数=点总数-最小点覆盖数=点总数-最大匹配数
最大匹配的必须边
所有最大匹配方案中都存在的边
最大匹配的可行边
某个最大匹配方案中存在,另一个最大匹配方案不存在的边
最大匹配的不可行边
所有最大匹配方案中都不存在的边
求法:
跑网络流得到最大匹配,在残余网络上流量未流满的边还可以走,反边可以走
跑tarjan,对于一条原图中的边
若两点所在不同的强连通分量且正边流量流满,则该边为必须边
还有一些二分图的经典应用:
最小路径覆盖问题
对于一个无向图,使得所有点被覆盖的最小简单路径(无环)数
对于这种问题
我们把原图的每一个点i拆点成i,i'两个点
对于原图的边(u,v)再新图中建边(u,v')
然后对于新建出来的二分图跑最大匹配即可
最后答案为原图总点数-最大匹配
这样建图的含义是
我们假定一开始用n(总点数)条路径覆盖了整个图
每一条匹配边,相当于合并了某两条路径
那么最终的答案即n-最大匹配
一般与网络流相关
练习题
Beautiful Graph
只有三种点权,奇奇偶,要求每条边相连的点奇偶性不一样
显然只有当该图为二分图时满足,有奇环就一定不能分配出奇偶不一致
我们首先跑二分图的判定
我们考虑对于一个二分图,可能其中有很多连通块
所有连通块之间互不影响,故方案数应相乘
对于其中一个连通块,我们可以钦定左边是2右边是1或3
或者反过来
设左边点数为k1,右边k2
这一个连通块答案应该是
左边每个点1,3任选一次和右边每一个点1,3任选一次
这个题目恶心的地方在于如果你每次memset可能吃不消
他第22个点是300000组数据,每个数据1个点
我们就每次只清1~n的数组就好了
然后就是sb题了
#include<bits/stdc++.h>
using namespace std;
const int maxn=300005,maxm=300005;
const int mod=998244353;
struct Edge{
int to,nxt;
}e[2*maxm];
int cnt;
int head[maxm];
long long pw[maxn];
int c[maxn];
int num[2];
int read(){
int x=0,y=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
return x*y;
}
void add(int u,int v){
e[cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt++;
return ;
}
bool dfs(int x,int co){
num[co-2]++;
c[x]=co;
for(int i=head[x];i!=-1;i=e[i].nxt){
int tmp=e[i].to;
if(c[tmp]==co)return 1;
if(c[tmp]==(co^1))continue;
if(dfs(tmp,co^1))return 1;
}
return 0;
}
void trash(int n){
cnt=0;
for(int i=1;i<=n;i++)head[i]=-1;
for(int i=1;i<=n;i++)c[i]=0;
return ;
}
int main(){
int tim,mxn=0;
tim=read();
pw[0]=1;
memset(head,-1,sizeof(head));
while(tim--){
int n,m;
long long ans=1;
n=read();m=read();
for(int i=mxn+1;i<=n;i++)pw[i]=pw[i-1]*2%mod;
mxn=max(mxn,n);
for(int i=1;i<=m;i++){
int u,v;
u=read();v=read();
add(u,v);
add(v,u);
}
bool flag=0;
for(int i=1;i<=n;i++){
if(c[i])continue;
num[0]=num[1]=0;
flag=dfs(i,2);
ans=(ans*(pw[num[0]]+pw[num[1]])%mod)%mod;
if(flag)break;
}
if(flag){printf("0\n");trash(n);continue;}
printf("%d\n",ans);
trash(n);
}
return 0;
}
Jamie's Contact Groups
二分答案,建图跑二分图的多重最大匹配
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<queue>
#include<sstream>
using namespace std;
const int maxn=1005,maxm=505,inf=0x3f3f3f3f;
struct Edge{
int to,w,nxt;
}e[maxn*maxm];
int cnt;
int head[maxn+maxm];
int n,m,s,t;
int lev[maxn+maxm];
vector<int>r[maxn];
queue<int>q;
int read(){
int x=0,y=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
return x*y;
}
void add(int u,int v,int w){
e[cnt].to=v;
e[cnt].w=w;
e[cnt].nxt=head[u];
head[u]=cnt++;
return ;
}
bool bfs(){
memset(lev,0,sizeof(lev));
while(!q.empty())q.pop();
q.push(s);
lev[s]=1;
while(!q.empty()){
int k=q.front();
q.pop();
for(int i=head[k];i!=-1;i=e[i].nxt){
int tmp=e[i].to;
if(e[i].w==0||lev[tmp])continue;
lev[tmp]=lev[k]+1;
q.push(tmp);
if(tmp==t)return 1;
}
}
return 0;
}
int dinic(int x,int flow){
if(x==t)return flow;
int rest=flow;
for(int i=head[x];i!=-1;i=e[i].nxt){
if(!rest)break;
int tmp=e[i].to;
if(e[i].w==0||lev[tmp]!=lev[x]+1)continue;
int inc=dinic(tmp,min(rest,e[i].w));
if(!inc)lev[tmp]=0;
e[i].w-=inc;
e[i^1].w+=inc;
rest-=inc;
}
return flow-rest;
}
bool check(int mid){
cnt=0;
memset(head,-1,sizeof(head));
s=n+m+1;t=n+m+2;
for(int i=1;i<=n;i++){
add(s,i,1);
add(i,s,0);
for(int j=0;j<r[i].size();j++){
int tmp=r[i][j];
add(i,tmp,inf);
add(tmp,i,0);
}
}
for(int i=1;i<=m;i++){
add(i+n,t,mid);
add(t,i+n,0);
}
int maxflow=0;
while(bfs()){
int flow=dinic(s,inf);
while(flow){
maxflow+=flow;
flow=dinic(s,inf);
}
}
if(maxflow==n)return 1;
return 0;
}
void solve(){
int l=0,r=n+1;
while(l+1<r){
int mid=l+((r-l)>>1);
if(check(mid))
r=mid;
else
l=mid;
}
printf("%d\n",r);
return ;
}
int main(){
while(1){
n=read();m=read();
if(n==0&&m==0)return 0;
for(int i=1;i<=n;i++){
r[i].clear();
int v;
stringstream ss;
string s;
getline(cin,s);
ss<<s;
ss>>s;
while(ss>>v)
r[i].push_back(v+n+1);
}
solve();
}
return 0;
}
Girls and Boys
二分图最大点独立集
但并未给出谁男谁女
其实我们不要慌,建边建双向边,跑匈牙利时给双方都算好匹配数组即可
#include<cstdio>
#include<cstring>
using namespace std;
const int maxn=505;
struct Edge{
int to,nxt;
}e[maxn*maxn];
int cnt;
int head[maxn];
int p[maxn];
bool vis[maxn];
int read(){
int x=0,y=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
return x*y;
}
void add(int u,int v){
e[cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt++;
return ;
}
int dfs(int x){
for(int i=head[x];i!=-1;i=e[i].nxt){
int tmp=e[i].to;
if(vis[tmp])continue;
vis[tmp]=1;
if((p[tmp]==0)||(dfs(p[tmp]))){
p[tmp]=x;
p[x]=tmp;
return 1;
}
}
return 0;
}
int main(){
int n;
while(scanf("%d",&n)!=EOF){
cnt=0;
memset(head,-1,sizeof(head));
memset(p,0,sizeof(p));
for(int i=1;i<=n;i++){
int u,m,v;
u=read()+1;m=read();
for(int j=1;j<=m;j++){
v=read()+1;
add(u,v);
add(v,u);
}
}
int ans=0;
for(int i=1;i<=n;i++){
if(p[i])continue;
memset(vis,0,sizeof(vis));
ans+=dfs(i);
}
printf("%d\n",n-ans);
}
return 0;
}
[HAOI2017]新型城市化
一句话题意,保证原图补图是个二分图,在原图中加入一条边能使原图最大团数至少加一的边有哪些
最大团数即使得选中的点集两两有边的最大点数
不会的同学建议学习一下
我们发现补图性质较为优秀,并且最大团求法就是在补图上应用的,把问题转移到补图上考虑
由于当补图为二分图时,原图最大团数=补图最大点独立集数
即在补图里删去一条边使得补图的最大点独立集数至少增加一
又由最大点独立集数等于总点数-最小点覆盖数=点总数-最大匹配数
问题进一步变成了在补图里删去一条边使得补图的最大匹配数至少减少一
我们想让补图的最大匹配数减少1,那么我们一定只能删去补图最大匹配的必须边
因为我们只能删一条边,删掉可行边或不可行边最大匹配不变
那么我们只要求出补图的最大匹配必须边即可
这就是一个经典问题了
对于补图用网络流跑最大匹配,残余网络再跑tarjan(即满流的边不能走,tarjan可走反边)
对于补图的某条边,它是必须边的条件是两个端点在不同的强连通分量里且网络流的残余网络里正边流满
即改变在这个最大匹配方案中且不可替代
码量还比较大,板子别打错了
#include<bits/stdc++.h>
using namespace std;
const int maxn=10005,maxm=150005,inf=0x3f3f3f3f;
struct Ans{
int x,y;
};
struct Edge{
int to,nxt;
}e[2*maxm];
struct EDGE{
int to,w,nxt;
}g[2*maxm+2*maxn];
int cnt1,cnt2;
int head[maxn],strt[maxn];
int c[maxn];
int s,t;
int lev[maxn];
int dfsnum=0,num=0;
int dfn[maxn],low[maxn];
int b[maxn];
bool vis[maxn];
queue<int>q;
stack<int>st;
vector<int>ans;
vector<Ans>ANS;
int read(){
int x=0,y=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')y=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
return x*y;
}
void add(Edge *e,int *head,int &cnt,int u,int v){
e[cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt++;
return ;
}
void add(EDGE *e,int *head,int &cnt,int u,int v,int w){
e[cnt].to=v;
e[cnt].w=w;
e[cnt].nxt=head[u];
head[u]=cnt++;
return ;
}
void dfs(int x,int co){
c[x]=co;
for(int i=head[x];i!=-1;i=e[i].nxt){
int tmp=e[i].to;
if(c[tmp])continue;
dfs(tmp,co^1);
}
return ;
}
bool bfs(){
memset(lev,0,sizeof(lev));
while(!q.empty())q.pop();
q.push(s);
lev[s]=1;
while(!q.empty()){
int k=q.front();
q.pop();
for(int i=strt[k];i!=-1;i=g[i].nxt){
int tmp=g[i].to;
if(g[i].w==0||lev[tmp])continue;
lev[tmp]=lev[k]+1;
q.push(tmp);
if(tmp==t)return 1;
}
}
return 0;
}
int dinic(int x,int flow){
if(x==t)return flow;
int rest=flow;
for(int i=strt[x];i!=-1;i=g[i].nxt){
if(!rest)break;
int tmp=g[i].to;
if(g[i].w==0||lev[tmp]!=lev[x]+1)continue;
int inc=dinic(tmp,min(rest,g[i].w));
if(!inc)lev[tmp]=0;
g[i].w-=inc;
g[i^1].w+=inc;
rest-=inc;
}
return flow-rest;
}
void tarjan(int x){
dfn[x]=low[x]=++dfsnum;
vis[x]=1;
st.push(x);
for(int i=strt[x];i!=-1;i=g[i].nxt){
int tmp=g[i].to;
if(g[i].w==0)continue;
if(!dfn[tmp]){
tarjan(tmp);
low[x]=min(low[x],low[tmp]);
}
else if(vis[tmp])
low[x]=min(low[x],low[tmp]);
}
if(dfn[x]==low[x]){
num++;
while(st.top()!=x){
int k=st.top();
st.pop();
vis[k]=0;
b[k]=num;
}
st.pop();
vis[x]=0;
b[x]=num;
}
return ;
}
int main(){
int n,m;
n=read();m=read();
s=n+1;t=n+2;
memset(head,-1,sizeof(head));
memset(strt,-1,sizeof(strt));
for(int i=1;i<=m;i++){
int u,v;
u=read();v=read();
add(e,head,cnt1,u,v);
add(e,head,cnt1,v,u);
}
for(int i=1;i<=n;i++){
if(c[i])continue;
dfs(i,2);
}
for(int i=1;i<=n;i++){
if(c[i]==3){
add(g,strt,cnt2,i,t,1);
add(g,strt,cnt2,t,i,0);
continue;
}
add(g,strt,cnt2,s,i,1);
add(g,strt,cnt2,i,s,0);
for(int j=head[i];j!=-1;j=e[j].nxt){
int tmp=e[j].to;
add(g,strt,cnt2,i,tmp,1);
add(g,strt,cnt2,tmp,i,0);
}
}
int maxflow=0;
while(bfs()){
int flow=dinic(s,inf);
while(flow){
maxflow+=flow;
flow=dinic(s,inf);
}
}
for(int i=1;i<=n+2;i++)
if(!dfn[i])
tarjan(i);
for(int i=1;i<=n;i++){
ans.clear();
for(int j=strt[i];j!=-1;j=g[j].nxt){
int tmp=g[j].to;
if(tmp<i||tmp>n||b[i]==b[tmp])continue;
if(((j%2==0)&&g[j].w==1)||((j&1)&&g[j^1].w==1))continue;
ans.push_back(tmp);
}
sort(ans.begin(),ans.end());
for(int j=0;j<ans.size();j++)
ANS.push_back((Ans){i,ans[j]});
}
printf("%d\n",ANS.size());
for(int i=0;i<ANS.size();i++)
printf("%d %d\n",ANS[i].x,ANS[i].y);
return 0;
}
