知识点
一个原始数组a[i]
定义一个差分数组b[i]=a[i]-a[i-1]
b[1]=a[1]-0,b[n+1]=0-a[n]
应用
1.b数组的前缀和就是a[i]
2.在a[l~r]增加k可以转化成b[l]+k,b[r+1]-k,求b的前缀和 =>将区间修改变为单点修改
关于时间复杂度
修改:O(1)
求前缀和:O(n)
我们先来看看差分
还有啥,后面还有比较恶心的树上差分
例题1 [USACO07JAN]区间统计Tallest Cow
基本上是个板子题,但一开始可能有点难理解
#include <bits/stdc++.h>
using namespace std;
const int maxn=10005;
int b[maxn];
bool vis[maxn][maxn];
int main()
{
int n,x,h,r;
scanf("%d%d%d%d",&n,&x,&h,&r);
b[1]=h;b[n+1]=-h;
for(int i=1;i<=r;i++){
int x,y;
scanf("%d%d",&x,&y);
if(x>y)swap(x,y);
if(!vis[x][y]){
b[x+1]--;b[y]++;
}
vis[x][y]=1;
}
long long ans=0;
for(int i=1;i<=n;i++){
ans+=b[i];
printf("%lld\n",ans);
}
return 0;
}
例题2 フェーン現象 (Foehn Phenomena)
代码
#include<bits/stdc++.h>
#define int long long//骚气宏定义
using namespace std;
const int maxn=200005;
int n,q,s,t;
long long a[maxn],b[maxn];
long long ans=0;
long long get(long long x){
if(x>0)return -(x*s);
if(x<0)return -(x*t);
return 0;
}
signed main()
{
scanf("%lld%lld%lld%lld",&n,&q,&s,&t);
for(int i=0;i<=n;i++){
scanf("%lld",&a[i]);
if(i>0)
b[i]=a[i]-a[i-1];
ans+=get(b[i]);
}
b[n+1]=0-a[n];
for(int i=1;i<=q;i++){
int l,r,x;
scanf("%lld%lld%lld",&l,&r,&x);
ans-=get(b[l]);//把从l-1到l点增加的温度减掉
b[l]+=x;
ans+=get(b[l]);//加上从l-1到l点新的增加的温度
if(r<n){
ans-=get(b[r+1]);
b[r+1]-=x;
ans+=get(b[r+1]);
}
printf("%lld\n",ans);
}
return 0;
}
例题3 P4552 [Poetize6] IncDec Sequence
啊咧,紫题
不慌,我们来分析分析
题目想让我们将一个序列的元素全都变相等
问最少操作次数和多少种结果
我们先抛开第二问,来看第一问
首先我们惊奇的发现所有元素都相等就是差分数组都等于0
当然b[1]不为0
我们随便给一组数据
2 5 3 6 2
2 3 -2 3 -4
那么这个差分数组大概就长上面这个模样
对于一个区间加1或减1,最优情况下是不是一个正数减1一个负数加1
这样显然能更快的接近0
所以我们应该去统计正数或负数的和的绝对值
可是这两个绝对值不一定相等啊
也就是说,当个小的哪一类数都变成0时,大的还剩些数
这时候怎么办?
我们应让这个改变值的区间[l,r]的某一端点在1或n
还是刚才那个例子
2 5 3 6 2
2 3 -2 3 -4
正数和的绝对值:7
负数和的绝对值:6
我们把差分数组里的负数解决掉后
两数组长这样
1 1 1 2 2
1 0 0 1 0
剩下第四个位置还没有解决
覆盖下区间[4,5] -1或区间[1,3] +1 即可
实际上,我们只关心做到b[2]~b[n]都是0的次数
而剩下的类似上面例子的b[4]我们一定可以用1次调整好
设正数和的绝对值为sum1,负数和的绝对值为sum2
答案应该就是
min(sum1,sum2)+max(sum1,sum2)-min(sum1,sum2)
=max(sum1,sum2)
在刚才的分析中应该不难发现这个序列最终的不同
应该取决于b[1]的值
因为b[1]=a[1]而a[1]=a[2]=a[3]..=a[n]
那么我们求b[1]的方案数即可
真正对b[1]有影响的应是我们第一问把无法正负配对的数解决掉时做的
因为在正负可以配对时我们对b[1]也就是a[1]的操作时必要的
可能有点难理解
而对于每一个无法正负配对的数我们都有两种选择
[i,n]或[1,i] 当我们选择后者时我们的方案就会多一个
那么sum1,和sum2的定义如上
第二问的答案应该是
max(sum1,sum2)-min(sum1,sum2)+1
= abs(sum1-sum2)+1
加1是因为我们把不变的情况减掉了
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn=100005;
long long a[maxn],b[maxn];
int main()
{
int n;
long long zs=0,fs=0;
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
b[i]=a[i]-a[i-1];
if(b[i]>0)zs+=b[i];
if(b[i]<0)fs-=b[i];
}
b[n+1]=0-a[n];
if(b[1]>0)zs-=b[1];
if(b[1]<0)fs+=b[1];
printf("%lld\n%lld",max(zs,fs),abs(zs-fs)+1);
return 0;
}
码量真是清新脱俗啊
练习 借教室
由于此题需要区间修改,我们很容易想到差分来处理
可是我们要找到从前往后第一次我们无法完成的申请(某个a[i]小于0)
可是这用差分数组判断不出来
用前缀和将每个数求出来就铁定超时了
那咋办?
我们注意到我们要求的是第一个我们无法完成的申请的编号
也就是说在这条申请前我们是都满足的
是不是在找一个临界点?
二分
怎么写判断函数呢?
我们只要判断在前mid个申请后无法完成
就让mid更小
否则我们让mid更大
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=1000005,maxm=1000005;
int n,m;
int a[maxn],b[maxn],c[maxn];
int s[maxm],t[maxm],d[maxm];
bool check(int x){
for(int i=1;i<=n;i++)b[i]=a[i]-a[i-1];
for(int i=1;i<=x;i++){
b[s[i]]-=d[i];
b[t[i]+1]+=d[i];
}
for(int i=1;i<=n;i++){
c[i]=c[i-1]+b[i];
if(c[i]<0)return 1;
}
return 0;
}
void search(){
int l=0,r=m+1;
while(l+1<r){
int mid=l+((r-l)>>1);
if(check(mid))
r=mid;
else
l=mid;
}
printf("%d",r);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=n;i++)b[i]=a[i]-a[i-1];
for(int i=1;i<=m;i++){
scanf("%d%d%d",&d[i],&s[i],&t[i]);
b[s[i]]-=d[i];b[t[i]+1]+=d[i];
}
bool flag=0;
for(int i=1;i<=n;i++){
c[i]=c[i-1]+b[i];
if(c[i]<0){flag=1;break;}
}
if(flag==0){printf("0");return 0;}
printf("-1\n");
search();
return 0;
}
练习&拓展 奶牛集会
前备知识:树状数组
这道题绕了我很久
可能是因为数学比较渣..
接下来是一波骚推导
这是原式
如果我们将奶牛的音亮从低到高排序这个max就可以不管了
下面的编号都是排序后的编号
若我们当前循环到i (1<=j< i)
将绝对值拆开(xi>xk,xi<xl,1<=k,l<i)
k=1~i-1中坐标X比Xi小的个数
l=1~i-1中坐标X比Xi大的个数
这个时候我们的任务应该就是去维护一个个数和坐标相关的值
树状数组可以做到
#include<bits/stdc++.h>
using namespace std;
const int maxn=20005,maxx=20005;
struct node{
int id;
int v,x;
bool operator <(node i)const{
return v<i.v;
}
}a[maxn];
int n,maxxx=0;
long long tree1[maxx],tree2[maxx];
long long ans=0;
int lowbit(int x){
return x&-x;
}
void update(int x,int val1,int val2){
while(x<=maxxx){
tree1[x]+=val1;
tree2[x]+=val2;
x+=lowbit(x);
}
}
long long query1(int x){
long long sum=0;
while(x){
sum+=tree1[x];
x-=lowbit(x);
}
return sum;
}
long long query2(int x){
long long sum=0;
while(x){
sum+=tree2[x];
x-=lowbit(x);
}
return sum;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d%d",&a[i].v,&a[i].x);
maxxx=max(maxxx,a[i].x);
}
sort(a+1,a+n+1);
for(int i=1;i<=n;i++){
update(a[i].x,a[i].x,1);
long long len=query2(a[i].x-1),dist1=query1(a[i].x-1),dist2=query1(maxxx);
ans+=a[i].v*(a[i].x*len-dist1+(dist2-dist1-a[i].x)-a[i].x*(i-1-len));
}
printf("%lld",ans);
return 0;
}
树形差分
下面的题很多都要用到lca
例题4 暗的连锁
本身就在lca的专题里..
第一眼看上去根本毫无思路啊!!
我们应该镇静点
首先,我们确定我们要切掉一条主要边和一条附加边
而我们不难看出,主要边就是树遍
对于任意一棵树来说我们随意切一条边都可以让这颗树不联通
有一条附加边呢?这时我们有几种可能,看一下下面的图
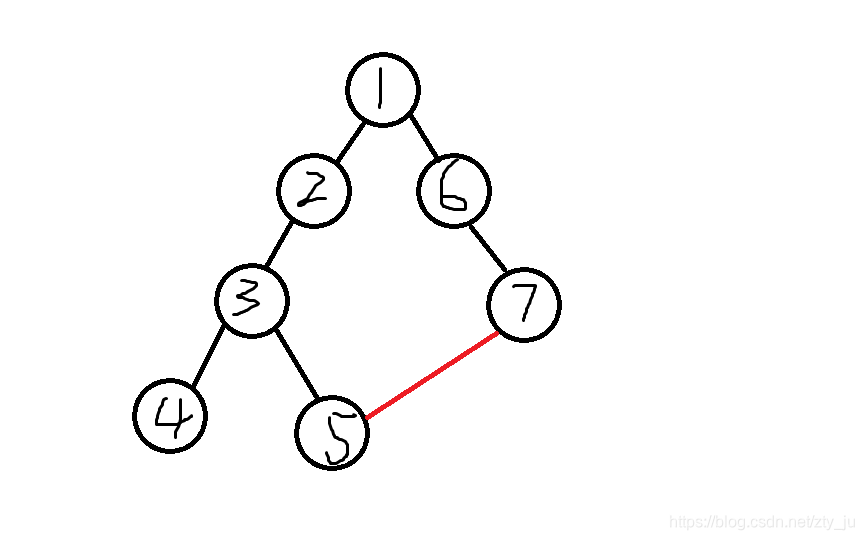
如上图红边为附加边
这时候我们在5-7这条树上路径上随便减一条主要边
就无法将这个图不连通了必须再删一条边
我们在这里给出了一个强壮度的定义
这条主要边删掉后最少还需删几条边才能使这个图不连通
由于我们最多删掉一条主要边和一条附加边
所以强壮度大于2的边我们是毫无办法的(因为这里要删3条边)
而强壮度为1的主要边我们只能再删与其对应的一条附加边
这条附加边就是与我们要删除的这条主要边构成环的唯一一条附加边(+1)
而强壮度为0的主要边我们再随便删一条附加边即可(+m)
但我们要找到附加边所构成环的原本的树上路径啊
lca登场
区间修改强壮度时间复杂度过高啊
树上差分登场
lca在这里就不细讲了
还是上面的图
从5-7添加一条附加边时强壮度增加的主要边同样是树上5-7的路径
这条路径上均会+1
边差分的话我们用b[i]对应i到其父亲的边的强壮度的差分数组
那么我们给b[5]++,b[7]++,b[lca(5,7)]-2即可
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=100005,maxm=200005;
int n,m,root=1;
int strong[maxn],c[maxn];
int deep[maxn],f[maxn][21];
vector<int>e[maxn];
void lca_pre(int x,int fa){
deep[x]=deep[fa]+1;
f[x][0]=fa;
for(int j=1;j<=20;j++){
if(deep[x]-(1<<j)>0)
f[x][j]=f[f[x][j-1]][j-1];
}
for(int i=0;i<e[x].size();i++){
int tmp=e[x][i];
if(tmp!=fa)
lca_pre(tmp,x);
}
}
int lca(int x,int y){
if(deep[x]<deep[y])swap(x,y);
for(int i=20;i>=0;i--){
if(deep[x]-(1<<i)>=deep[y])
x=f[x][i];
}
if(x==y)return x;
for(int i=20;i>=0;i--){
if(f[x][i]!=f[y][i]){
x=f[x][i];
y=f[y][i];
}
}
return f[x][0];
}
void check(int x,int fa){
c[x]=strong[x];
for(int i=0;i<e[x].size();i++){
int tmp=e[x][i];
if(tmp!=fa){
check(tmp,x);
c[x]+=c[tmp];
}
}
}
int main()
{
long long ans=0;
scanf("%d%d",&n,&m);
for(int i=1;i<n;i++){
int u,v;
scanf("%d%d",&u,&v);
e[u].push_back(v);
e[v].push_back(u);
}
lca_pre(root,0);
for(int i=1;i<=m;i++){
int u,v;
scanf("%d%d",&u,&v);
if(u==v)continue;
int k=lca(u,v);
strong[u]++;strong[v]++;
strong[k]-=2;
}
check(root,0);
for(int i=1;i<=n;i++){
if(i==root)continue;
if(c[i]==0)ans+=m;
else if(c[i]==1)ans++;
}
printf("%lld",ans);
return 0;
}
练习 [JLOI2014]松鼠的新家
可以做做,我用的是点差分
#include <bits/stdc++.h>
using namespace std;
const int maxn=300005,maxm=300005;
struct node{
int to;
int nxt;
}e[2*maxm];
int cnt=0;
int head[maxn];
int a[maxn],b[maxn];
int deep[maxn];
int f[maxn][21];
int ans[maxn];
void add(int u,int v){
e[cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt++;
}
void lca_pre(int x,int fa){
deep[x]=deep[fa]+1;
f[x][0]=fa;
for(int j=1;j<=20;j++){
if(deep[x]-(1<<j)>0)
f[x][j]=f[f[x][j-1]][j-1];
}
for(int i=head[x];i!=-1;i=e[i].nxt){
int tmp=e[i].to;
if(tmp!=fa)
lca_pre(tmp,x);
}
}
int lca(int x,int y){
if(deep[x]<deep[y])swap(x,y);
for(int i=20;i>=0;i--){
if(deep[x]-(1<<i)>=deep[y])
x=f[x][i];
}
if(x==y)return x;
for(int i=20;i>=0;i--){
if(f[x][i]!=f[y][i]){
x=f[x][i];
y=f[y][i];
}
}
return f[x][0];
}
void dfs(int x,int fa){
ans[x]=b[x];
for(int i=head[x];i!=-1;i=e[i].nxt){
int tmp=e[i].to;
if(tmp!=fa){
dfs(tmp,x);
ans[x]+=ans[tmp];
}
}
}
int main()
{
int n;
scanf("%d",&n);
memset(head,-1,sizeof(head));
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<n;i++){
int u,v;
scanf("%d%d",&u,&v);
add(u,v);
add(v,u);
}
lca_pre(1,0);
for(int i=2;i<=n;i++){
int k=lca(a[i],a[i-1]);
b[f[k][0]]--;
b[k]--;
b[a[i]]++;b[a[i-1]]++;
}
dfs(1,0);
for(int i=2;i<=n;i++)ans[a[i]]--;
for(int i=1;i<=n;i++)
printf("%d\n",ans[i]);
return 0;
}
练习 运输计划
这道题我们要求的是最长的一条路径最短
震惊,最大值最小化
用二分
这就是我们一开始的思路
怎样写判断条件呢?
我们只要看所有大于mid的遍在用一个虫洞后能否全部小于等于mid
这时候就可以用差分来区间修改了
#include<bits/stdc++.h>
using namespace std;
const int maxn=300005;
struct node{
int to,w;
int nxt;
}e[2*maxn];
int n,m,dfsnum=0;
int maxt=0,maxd=0;
int cnt=0;
int head[maxn];
int dfn[maxn];
int u[maxn],v[maxn],k[maxn];
int deep[maxn];
int f[maxn][21];
int c[maxn];
int dis[maxn],dist[maxn],edge[maxn];
void add(int u,int v,int w){
e[cnt].to=v;
e[cnt].w=w;
e[cnt].nxt=head[u];
head[u]=cnt++;
}
void lca_pre(int x,int fa){
dfn[++dfsnum]=x;
deep[x]=deep[fa]+1;
f[x][0]=fa;
for(int j=1;j<=20;j++){
if(deep[x]-(1<<j)>0)
f[x][j]=f[f[x][j-1]][j-1];
}
for(int i=head[x];i!=-1;i=e[i].nxt){
int tmp=e[i].to;
if(tmp!=fa){
dis[tmp]=dis[x]+e[i].w;
edge[tmp]=e[i].w;
lca_pre(tmp,x);
}
}
}
int lca(int x,int y){
if(deep[x]<deep[y])swap(x,y);
for(int i=20;i>=0;i--){
if(deep[x]-(1<<i)>=deep[y])
x=f[x][i];
}
if(x==y)return x;
for(int i=20;i>=0;i--){
if(f[x][i]!=f[y][i]){
x=f[x][i];
y=f[y][i];
}
}
return f[x][0];
}
bool check(int x){
memset(c,0,sizeof(c));
int sum=0;
for(int i=1;i<=m;i++){
if(dist[i]>x){
c[k[i]]-=2;
c[u[i]]++;
c[v[i]]++;
sum++;
}
}
for(int i=n;i>=1;i--){
c[f[dfn[i]][0]]+=c[dfn[i]];
if(maxd-edge[dfn[i]]<=x&&c[dfn[i]]==sum)
return 1;
}
return 0;
}
void search(){
int l=maxd-maxt-1,r=maxd+1;
while(l+1<r){
int mid=l+((r-l)>>1);
if(check(mid))
r=mid;
else
l=mid;
}
printf("%d",r);
}
int main()
{
scanf("%d%d",&n,&m);
memset(head,-1,sizeof(head));
for(int i=1;i<n;i++){
int a,b,t;
scanf("%d%d%d",&a,&b,&t);
add(a,b,t);
add(b,a,t);
maxt=max(maxt,t);
}
lca_pre(1,0);
for(int i=1;i<=m;i++){
scanf("%d%d",&u[i],&v[i]);
k[i]=lca(u[i],v[i]);
dist[i]=dis[u[i]]+dis[v[i]]-dis[k[i]]*2;
maxd=max(maxd,dist[i]);
// cout<<dis[u[i]]<<" "<<dis[v[i]]<<" "<<dis[k[i]]<<" "<<dist[i]<<endl;
}
search();
return 0;
}
练习 [USACO15DEC]最大流Max Flow
基本是一个套路,多练几个题
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=50005;
struct Edge{
int to;
int nxt;
}e[2*maxn];
int cnt=0;
int head[maxn];
int b[maxn],c[maxn];
int deep[maxn];
int f[maxn][21];
void add(int u,int v){
e[cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt++;
}
void lca_pre(int x,int fa){
deep[x]=deep[fa]+1;
f[x][0]=fa;
for(int i=1;i<=20;i++){
if(deep[x]-(1<<i)>0)
f[x][i]=f[f[x][i-1]][i-1];
}
for(int i=head[x];i!=-1;i=e[i].nxt){
int tmp=e[i].to;
if(tmp!=fa)
lca_pre(tmp,x);
}
}
int lca(int x,int y){
if(deep[x]<deep[y])swap(x,y);
for(int i=20;i>=0;i--){
if(deep[x]-(1<<i)>=deep[y])
x=f[x][i];
}
if(x==y)return x;
for(int i=20;i>=0;i--){
if(f[x][i]!=f[y][i]){
x=f[x][i];
y=f[y][i];
}
}
return f[x][0];
}
void dfs(int x,int fa){
c[x]=b[x];
for(int i=head[x];i!=-1;i=e[i].nxt){
int tmp=e[i].to;
if(tmp!=fa){
dfs(tmp,x);
c[x]+=c[tmp];
}
}
}
int main()
{
int n,k,root=1,ans=0;
scanf("%d%d",&n,&k);
memset(head,-1,sizeof(head));
for(int i=1;i<n;i++){
int x,y;
scanf("%d%d",&x,&y);
add(x,y);
add(y,x);
}
lca_pre(root,0);
for(int i=1;i<=k;i++){
int s,t;
scanf("%d%d",&s,&t);
int l=lca(s,t);
b[s]++;b[t]++;
b[l]--;b[f[l][0]]--;
//这里在lca减一次和lca的父亲减一次的意义是:
//lca这个点只需加1次可递归上来时我们多加了一次,把这次减掉后lca的父亲就只要减1次了
}
dfs(root,0);
for(int i=1;i<=n;i++)
ans=max(ans,c[i]);
printf("%d",ans);
return 0;
}
